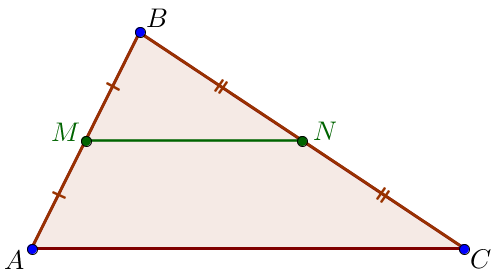
В треугольнике \(\displaystyle ABC\) отмечены середины \(\displaystyle M\) и \(\displaystyle N\) сторон \(\displaystyle BC\) и \(\displaystyle AC\) соответственно. Площадь треугольника \(\displaystyle CNM\) равна \(\displaystyle 57 {\small.}\) Найдите площадь четырёхугольника \(\displaystyle ABMN {\small.}\)
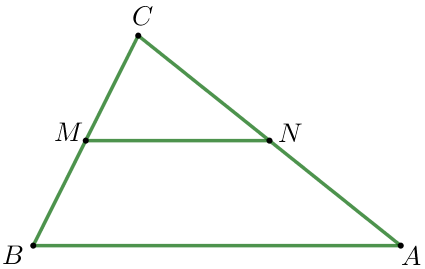
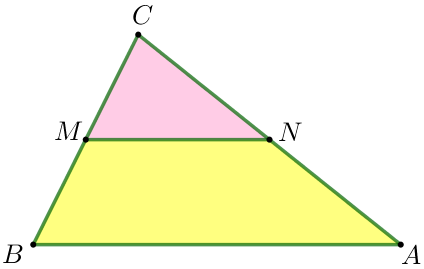 | Площадь четырёхугольника \(\displaystyle ABMN \) равна разности площадей треугольников \(\displaystyle ABC\) и \(\displaystyle CNM {\small:}\) \(\displaystyle S_{ABMN}=S_{\triangle ABC}-S_{\triangle CNM} {\small.}\)
|
Так как точки \(\displaystyle M\) и \(\displaystyle N\) – середины сторон \(\displaystyle BC\) и \(\displaystyle AC\) соответственно, то \(\displaystyle MN\) – средняя линия треугольника \(\displaystyle ABC {\small.}\)
\(\displaystyle MN \parallel AB\) и \(\displaystyle MN=\frac{1}{2}\cdot AB\small. \)
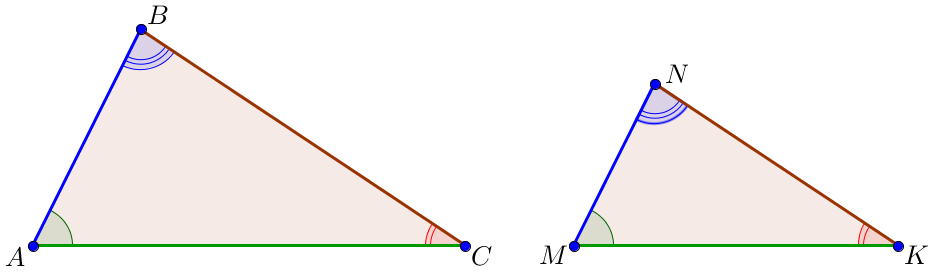
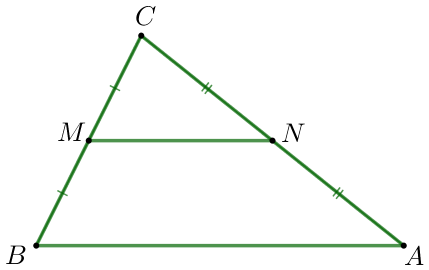 | Рассмотрим треугольники \(\displaystyle CNM\) и \(\displaystyle ABC {\small:} \\ \) \(\displaystyle \frac{CM}{BC}= \frac{CN}{AC}=\frac{MN}{AB}=\frac{1}{2}\small. \) |
В подобных треугольниках коэффициент подобия \(\displaystyle k\) равен отношению сходственных сторон. Значит,
\(\displaystyle k=\frac{MN}{AB}=\frac{1}{2} {\small.} \)
\(\displaystyle \frac{S_{\triangle CNM}}{S_{\triangle ABC}}=k^2 {\small,} \\ \)
\(\displaystyle S_{\triangle ABC}=\frac{{S_{\triangle CNM}}}{k^2}{\small,} \\ \)
\(\displaystyle S_{\triangle ABC}=\frac{S_{\triangle CNM}}{{\big(\frac{1}{2}\big)}^2}=\frac{S_{\triangle CNM}}{\frac{1}{4}}=4\cdot S_{\triangle CNM}{\small.} \\ \)
Получаем
\(\displaystyle S_{ABMN}=S_{\triangle ABC}-S_{\triangle CNM} =4\cdot S_{\triangle CNM}- S_{\triangle CNM}=3\cdot S_{\triangle CNM}{\small,}\\ \)
\(\displaystyle S_{ABMN}=3\cdot 57=171{\small.}\)
Ответ: \(\displaystyle 171 {\small.}\)