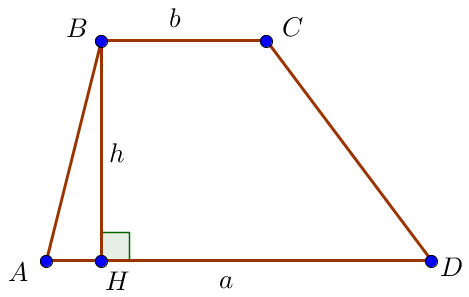
Найдите площадь трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD\) и \(\displaystyle BC{\small,}\) если \(\displaystyle AD=11{\small,}\) \(\displaystyle BC=6{\small,}\) \(\displaystyle CD=12\) и \(\displaystyle \angle D=30^{\circ}{\small.}\)
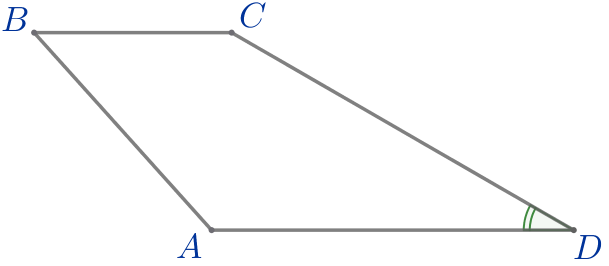
Обозначим на рисунке известные измерения.
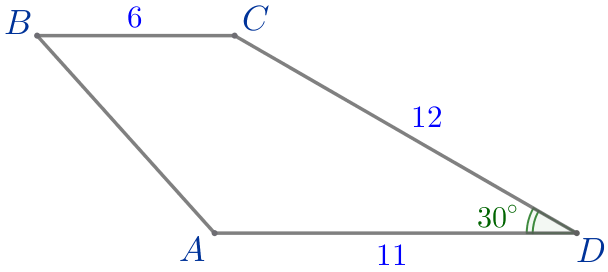 | \(\displaystyle ABCD\) – трапеция:
|
Требуется найти площадь трапеции \(\displaystyle ABCD{\small.}\)
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2} \cdot h{\small,}\)
где \(\displaystyle h\) – высота трапеции.
Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH{\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle CHD{\small.}\)
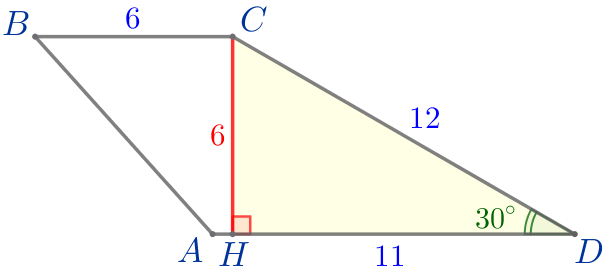 | В прямоугольном треугольнике напротив угла \(\displaystyle 30^{\circ}\) лежит катет равный половине гипотенузы, значит, \(\displaystyle CH=\frac{1}{2}\cdot CD=\frac{1}{2}\cdot 12=6{\small.}\) |
В результате получаем:
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2} \cdot CH=\frac{11+6}{2} \cdot 6=\frac{17 \cdot 6}{2}=51{\small.}\)
Ответ: \(\displaystyle 51{\small.}\)