Найдите площадь равнобедренной трапеции, если её основания равны \(\displaystyle 7\) и \(\displaystyle 23{\small,}\) а один из углов равен \(\displaystyle 45^{\circ}{\small.}\)
Обозначим на рисунке вершины трапеции и известные измерения.
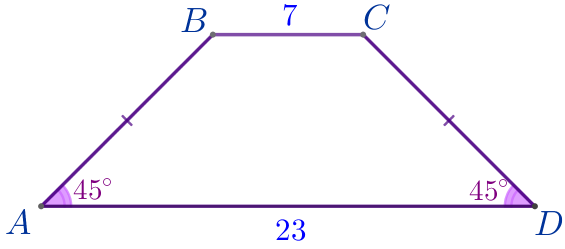 | \(\displaystyle ABCD\) – трапеция:
\(\displaystyle \angle A=\angle D=45^{\circ}{\small.}\) |
Требуется найти площадь трапеции \(\displaystyle ABCD{\small.}\)
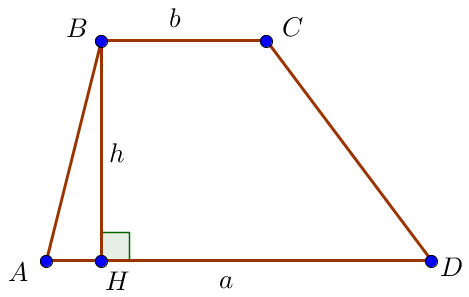
\(\displaystyle S_{ABCD}=\frac{AD+BC}{2} \cdot h{\small,}\)
где \(\displaystyle h\) – высота трапеции.
То есть
\(\displaystyle S_{ABCD}=\frac{23+7}{2} \cdot h=15 \cdot h{\small.}\)
Найдём высоту трапеции.
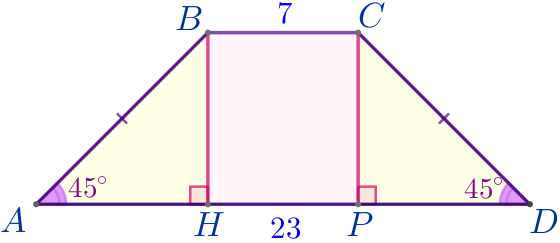 | Из вершин \(\displaystyle B\) и \(\displaystyle C\) проведём высоты \(\displaystyle BH\) и \(\displaystyle CP{\small.}\) В результате получили прямоугольник \(\displaystyle BCPH\) и два прямоугольных треугольника \(\displaystyle ABH\) и \(\displaystyle DCP{\small.}\) |
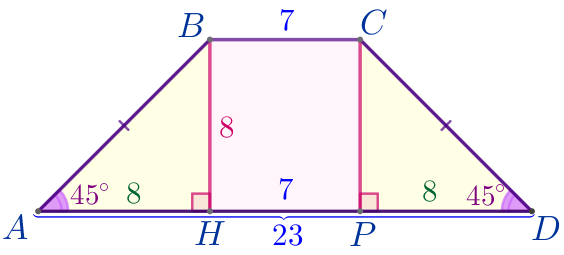 | \(\displaystyle \color{red}{\bf1)}\) В прямоугольнике \(\displaystyle BCPH\) противоположные стороны равны, значит, \(\displaystyle HP=BC=7{\small.}\) |
\(\displaystyle \color{red}{\bf2)}\) Прямоугольные треугольники \(\displaystyle ABH\) и \(\displaystyle DCP\) равны по гипотенузе \(\displaystyle (AB=CD)\) и острому углу \(\displaystyle (\angle A=\angle D=45^{\circ}){\small,}\) значит,
\(\displaystyle AH=DP=\frac{AD-HP}{2}=\frac{23-7}{2}=\frac{16}{2}=8{\small.}\)
\(\displaystyle \color{red}{\bf3)}\) Прямоугольный треугольник \(\displaystyle ABH\) с острым углом \(\displaystyle 45^{\circ}\) является равнобедренным, значит,
\(\displaystyle BH=AH=8{\small.}\)
То есть высота трапеции \(\displaystyle ABCD\) равна \(\displaystyle 8{\small.}\)
Подставим \(\displaystyle h=8\) в формулу площади трапеции:
\(\displaystyle S_{ABCD}=15 \cdot h=15 \cdot 8=120{\small.}\)
Ответ: \(\displaystyle 120{\small.}\)