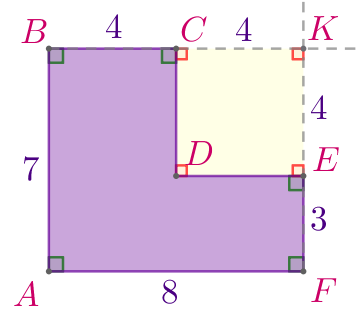
Найдите площадь прямоугольной фигуры, изображенной на рисунке.
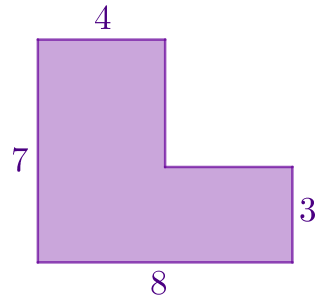
Обозначим вершины фигуры буквами и укажем на рисунке прямые углы данного многоугольника.
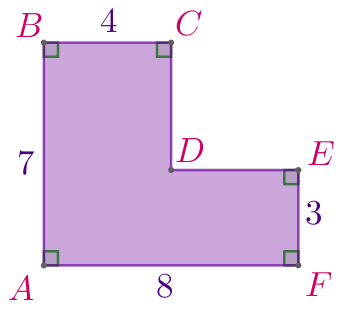 | \(\displaystyle ABCDEF\) – многоугольник:
Требуется найти площадь данной фигуры. |
Продлим стороны \(\displaystyle BC\) и \(\displaystyle FE\) за точки \(\displaystyle C\) и \(\displaystyle E\) соответственно.
Точку пересечения прямых \(\displaystyle BC\) и \(\displaystyle FE\) обозначим буквой \(\displaystyle K{\small.}\)
\(\displaystyle ABKF\) – прямоугольник.
\(\displaystyle CKED\) – прямоугольник. | 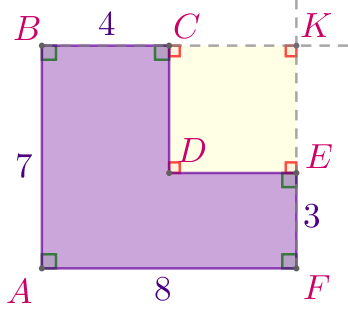 |
По свойству площади площадь \(\displaystyle S\) фигуры \(\displaystyle ABCDEF\) найдём как разность площадей двух прямоугольников \(\displaystyle ABKF\) и \(\displaystyle CKED{\small:}\)
\(\displaystyle S=S_{ABKF}-S_{CKED}{\small.}\)
\(\displaystyle S_{ABKF}=56{\small.}\)
\(\displaystyle S_{CKED}=16{\small.}\)
В результате получаем:
\(\displaystyle S=S_{ABKF}-S_{CKED}=56-16=40{\small.}\)
Ответ: \(\displaystyle 40{\small.}\)