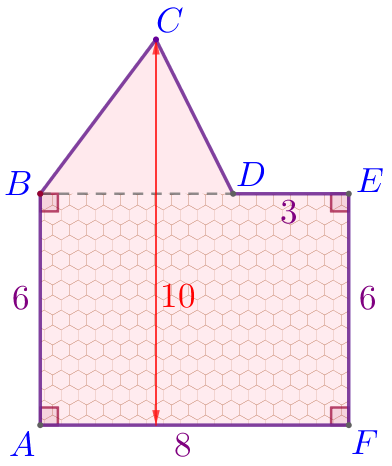
Найдите площадь фигуры, изображённой на рисунке, у которой три угла прямые.
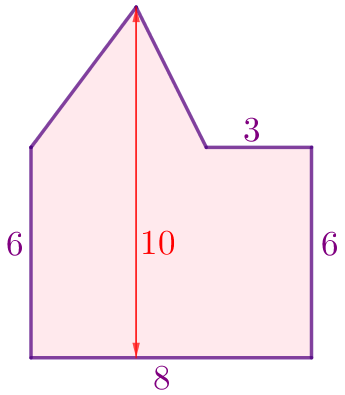
Обозначим вершины фигуры буквами и укажем на рисунке прямые углы данного многоугольника.
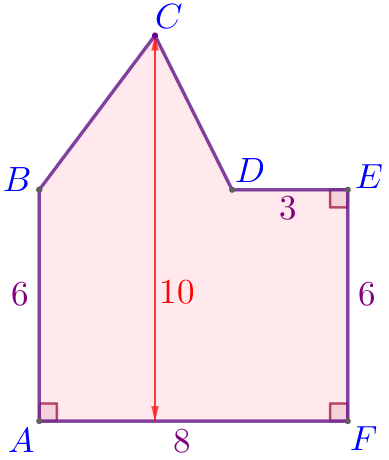 | \(\displaystyle ABCDEF\) – многоугольник:
Требуется найти площадь данной фигуры. |
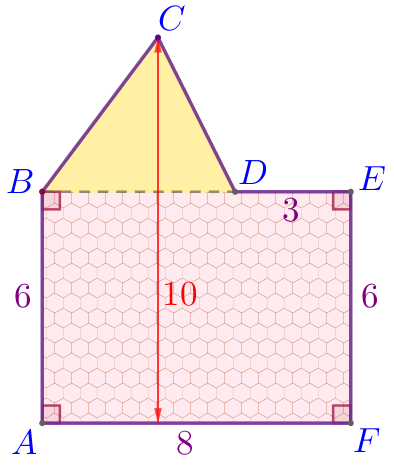 | По свойству площади площадь \(\displaystyle S\) фигуры \(\displaystyle ABCDEF\) найдём как сумму площадей прямоугольника \(\displaystyle ABEF\) и треугольника \(\displaystyle BCD{\small:}\) \(\displaystyle S=S_{ABEF}+S_{BCD}{\small.}\) |
\(\displaystyle S_{ABEF}=48{\small.}\)
\(\displaystyle S_{BCD}=10{\small.}\)
В треугольнике \(\displaystyle BCD\) из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH\) к основанию \(\displaystyle BD{\small.}\) Тогда
\(\displaystyle S_{BCD}=\frac{1}{2} \cdot BD\cdot CH{\small.}\)
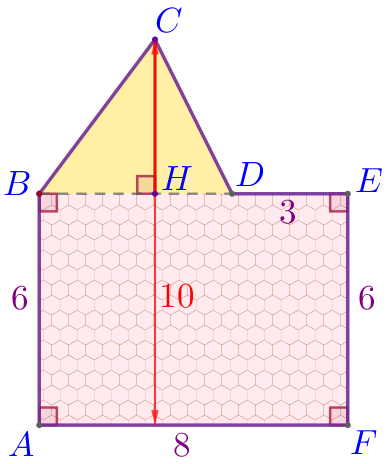 |
\(\displaystyle CH=10-6=4{\small.}\) |
Значит,
\(\displaystyle S_{BCD}=\frac{1}{2} \cdot BD\cdot CH=\frac{1}{2} \cdot 5 \cdot 4=10{\small.}\)
В результате получаем:
\(\displaystyle S=S_{ABEF}+S_{BCD}=48+10=58{\small.}\)
Ответ: \(\displaystyle 58{\small.}\)