Составьте верное равенство:
\(\displaystyle \tg 30^{\circ}=\)
СПОСОБ 1
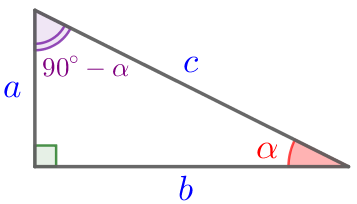 | Рассмотрим прямоугольный треугольник с катетами \(\displaystyle a{\small,}\) \(\displaystyle b\) и гипотенузой \(\displaystyle c{\small.}\) Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Пусть один острый угол прямоугольного треугольника равен \(\displaystyle \color{red}{\alpha}{\small,}\) тогда второй острый угол равен \(\displaystyle (\color{darkviolet}{90^{\circ}-\alpha}){\small.}\) |
Запишем тригонометрические функции для углов \(\displaystyle \color{red}{\alpha}\) и \(\displaystyle (\color{darkviolet}{90^{\circ}-\alpha})\) по определению (через отношение сторон прямоугольного треугольника):
\(\displaystyle \sin \color{red}{\alpha}=\frac{\color{blue}{a}}{\color{blue}{c}}=\cos(\color{darkviolet}{90^{\circ}-\alpha})\\ \)
\(\displaystyle \cos \color{red}{\alpha}=\frac{\color{blue}{b}}{\color{blue}{c}}=\sin(\color{darkviolet}{90^{\circ}-\alpha})\\ \)
\(\displaystyle \tg \color{red}{\alpha}=\frac{\color{blue}{a}}{\color{blue}{b}}=\ctg (\color{darkviolet}{90^{\circ}-\alpha})\\ \)
\(\displaystyle \ctg \color{red}{\alpha}=\frac{\color{blue}{b}}{\color{blue}{a}}=\tg (\color{darkviolet}{90^{\circ}-\alpha})\)
По формулам приведения получаем
\(\displaystyle \tg 30^{\circ}=\ctg (90^{\circ}-30^{\circ})=\ctg 60^{\circ}{\small.}\)
СПОСОБ 2
| \(\displaystyle \alpha\) | \(\displaystyle 30^{\circ}\) | \(\displaystyle 45^{\circ}\) | \(\displaystyle 60^{\circ}\) |
| \(\displaystyle \sin \alpha\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{\sqrt{3}}{2}\) |
| \(\displaystyle \cos \alpha\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{1}{2}\) |
| \(\displaystyle \tg \alpha\) | \(\displaystyle \frac{1}{\sqrt{3}}\) | \(\displaystyle 1\) | \(\displaystyle \sqrt{3}\) |
| \(\displaystyle \ctg \alpha\) | \(\displaystyle \sqrt{3}\) | \(\displaystyle 1\) | \(\displaystyle \frac{1}{\sqrt{3}}\) |
По таблице видим, что \(\displaystyle \tg 30^{\circ}=\frac{1}{\sqrt{3}}\) и \(\displaystyle \ctg 60^{\circ}=\frac{1}{\sqrt{3}}{\small.}\) Значит,
\(\displaystyle \tg 30^{\circ}=\ctg 60^{\circ}{\small.}\)
Ответ: \(\displaystyle \tg 30^{\circ}=\ctg 60^{\circ}{\small.}\)