На рисунке изображены несколько отрезков, соединяющих точку \(\displaystyle O\) с точками \(\displaystyle E{\small ,}\) \(\displaystyle D{\small ,}\) \(\displaystyle C{\small ,}\) \(\displaystyle B\) и \(\displaystyle A\) на прямой \(\displaystyle a{\small .}\)
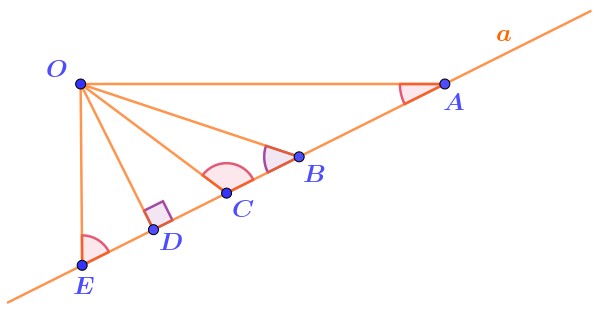
Какой из этих отрезков является перпендикуляром к прямой \(\displaystyle a{\small ?}\)
Проверяем выполнение требований определения перпендикуляра:
\(\displaystyle \,\,\,\,\,\,\,\,\,\)1) по условию точка \(\displaystyle D\) принадлежит прямой \(\displaystyle a{\small ;}\)
\(\displaystyle \,\,\,\,\,\,\,\,\,\)2) прямая \(\displaystyle OD\) перпендикулярна к прямой \(\displaystyle a{\small ,\;}\)так как угол \(\displaystyle ODA\) на рисунке отмечен как прямой.
Значит, отрезок \(\displaystyle OD\)– перпендикуляр к прямой \(\displaystyle a{\small .}\)
Другие отрезки не удовлетворяют условиям определения перпендикуляра к прямой.
Ответ: \(\displaystyle OD{\small .}\)