Отрезки \(\displaystyle AP\) и \(\displaystyle BQ\) \(\displaystyle -\) перпендикуляры к прямой \(\displaystyle PQ{\small .}\) Точка \(\displaystyle C\) принадлежит прямой \(\displaystyle BP{\small .}\)
Известно: \(\displaystyle AP=BQ=5\), \(\displaystyle \angle PAQ=39\degree {\small .}\)
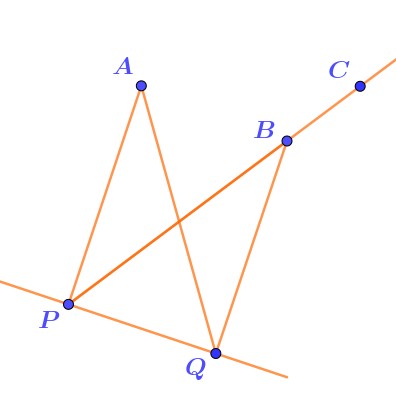
Найти величину угла \(\displaystyle CBQ{\small .}\) Ответ дайте в градусах.
\(\displaystyle \angle CBQ=\)\(\displaystyle \degree \)
Дополним рисунок обозначениями равных элементов и прямых углов.
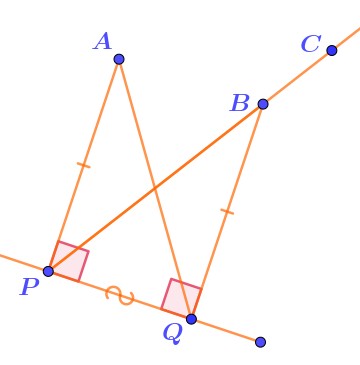
\(\displaystyle \left\{\begin{array}{ll}AP=BQ\text{ \footnotesize \it (по условию)}\\PQ -\text{ \footnotesize\it общая сторона}\\\angle APQ=\angle BQP\text{ \footnotesize \it (по определению перпендикуляра)}\end{array} {\LARGE\Rightarrow}\quad\begin{array}{c} \\{\bf\triangle}PAQ={\bf\triangle}QBP\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
В равных треугольниках равны углы, расположенные против общей стороны:
\(\displaystyle \angle QBP=\angle PAQ=39\degree {\small .}\)
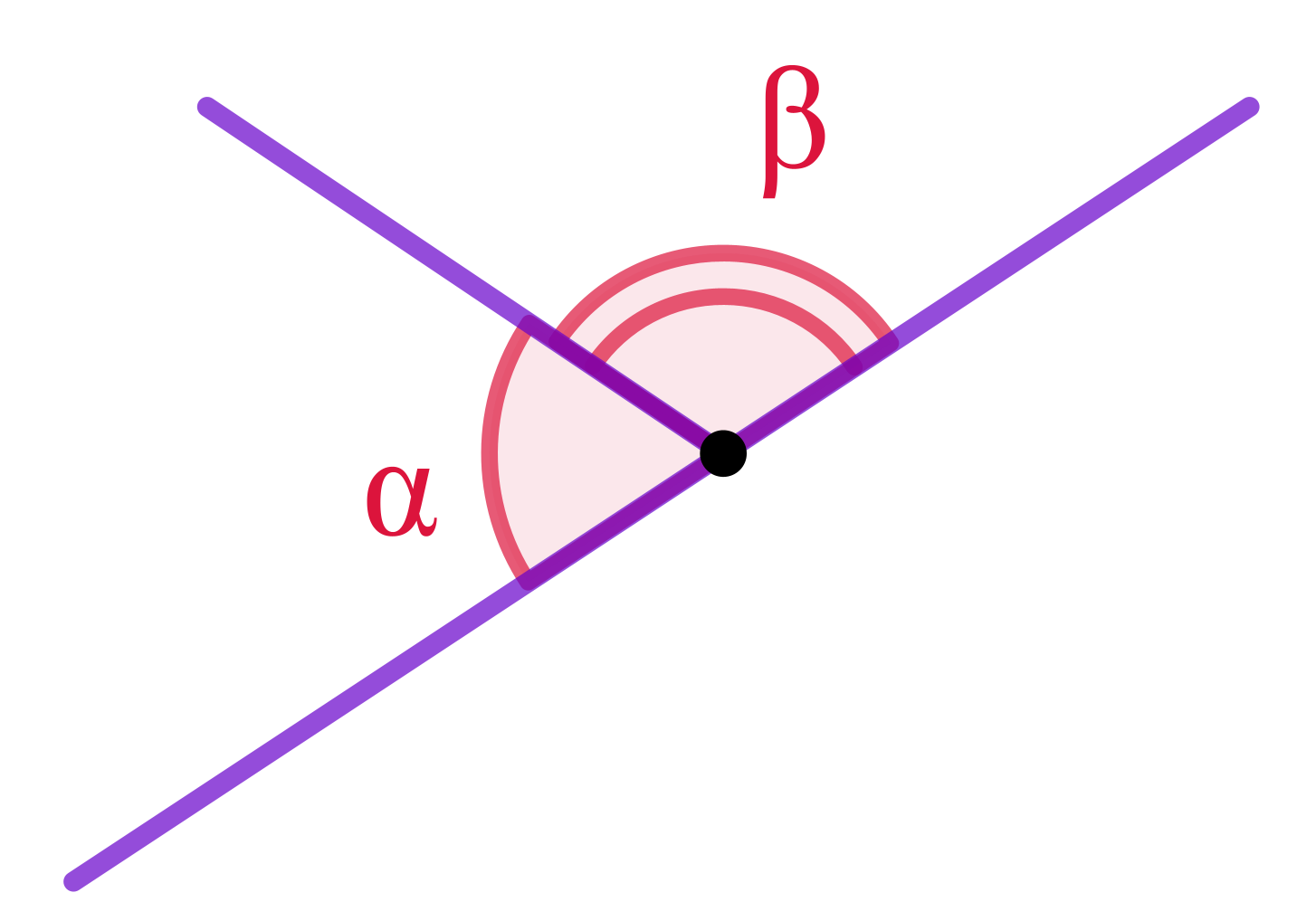
По свойству смежных углов
\(\displaystyle \angle CBQ+\angle QBP=180\degree{\small .}\)
Откуда
\(\displaystyle \angle CBQ=180\degree -\angle QBP=180\degree -39\degree =\)\(\displaystyle 141\degree {\small .}\)
Ответ: \(\displaystyle 141\degree {\small .}\)