В треугольнике \(\displaystyle ABC\) угол при вершине \(\displaystyle C\) прямой.
Какие из следующих утверждений верны?
Изобразим произвольный прямоугольный треугольник \(\displaystyle ABC\) с прямым углом \(\displaystyle C{\small .}\)
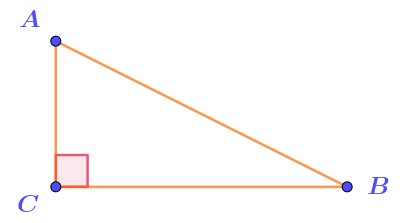
Для отрезка \(\displaystyle AC\) выполняются условия определения перпендикуляра к прямой:
1) точка \(\displaystyle C\) принадлежит прямой \(\displaystyle CB\);
2) угол \(\displaystyle ACB\) отмечен как прямой, значит отрезок \(\displaystyle AC\) лежит на прямой, перпендикулярной к прямой \(\displaystyle CB\).
Для отрезка \(\displaystyle BC\) также выполняются условия определения перпендикуляра к прямой.
Значит верны утверждения:
отрезок \(\displaystyle AC\) является перпендикуляром к прямой \(\displaystyle BC{\small ,}\)
отрезок \(\displaystyle BC\) является перпендикуляром к прямой \(\displaystyle CA{\small .}\)