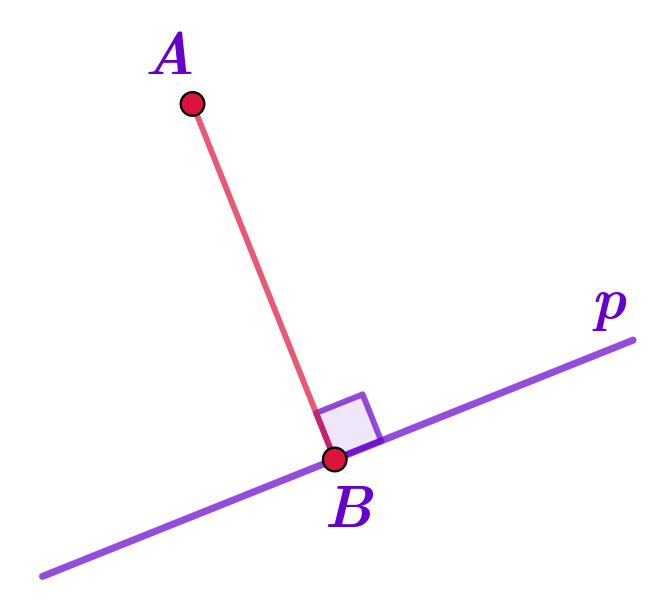
Отрезок \(\displaystyle PH\,-\) перпендикуляр к прямой \(\displaystyle a{\small ,}\)\(\displaystyle Q\in PH{\small .}\)
Известно, что \(\displaystyle PH=7\,\footnotesize {см}{\small ,}\) \(\displaystyle PQ =3\,\footnotesize {см}{\small .}\)
Найти длину перпендикуляра, опущенного из точки \(\displaystyle Q\) на прямую \(\displaystyle a{\small .}\) Ответ дайте в сантиметрах.
\(\displaystyle \footnotesize {см}\)
Изобразим рисунок.
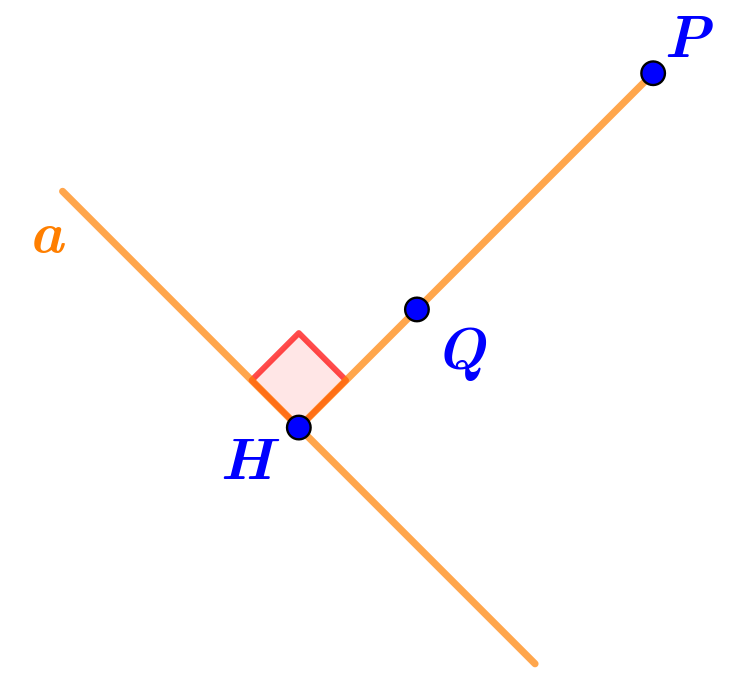
1. Отрезок \(\displaystyle PH\,-\) перпендикуляр к прямой \(\displaystyle a{\small .}\)
Отметим на рисунке прямой угол: прямые \(\displaystyle PH\) и \(\displaystyle a\) перпендикулярны по определению перпендикуляра.
2. Отрезок \(\displaystyle QH\) часть прямой \(\displaystyle PH{\small ,}\) перпендикулярной прямой \(\displaystyle a\), точка \(\displaystyle H\) принадлежит прямой \(\displaystyle a{\small .}\)
Значит, по определению, \(\displaystyle QH\) и есть перпендикуляр к прямой \(\displaystyle a{\small .}\)
3. Длина отрезка \(\displaystyle PH\) равна сумме длин его частей:
\(\displaystyle PH = PQ + QH{\small .}\)
По условию
\(\displaystyle PH=7\,\footnotesize {см}{\small ,}\) \(\displaystyle PQ=3\,\footnotesize {см}{\small .}\)
Подставим известные длины отрезков \(\displaystyle PH{\small ,}\)\(\displaystyle PQ\) и найдём длину отрезка \(\displaystyle QH{\small :}\)
\(\displaystyle 7 = 4+ QH{\small ,}\)
\(\displaystyle QH=4\,\footnotesize {см}{\small .}\)
Ответ: \(\displaystyle 4\,\footnotesize {см}{\small .}\)