В треугольнике \(\displaystyle ABC\) провели медиану \(\displaystyle CM\small.\) Найдите длину \(\displaystyle BC\small,\) если \(\displaystyle AB=6\small,\) \(\displaystyle CM=5\) и \(\displaystyle \angle BMC=60^{\circ}\small.\)
Поскольку \(\displaystyle MC\) медиана, то \(\displaystyle AM=BM=\frac{AB}{2}=\frac{6}{2}=3\small.\) | 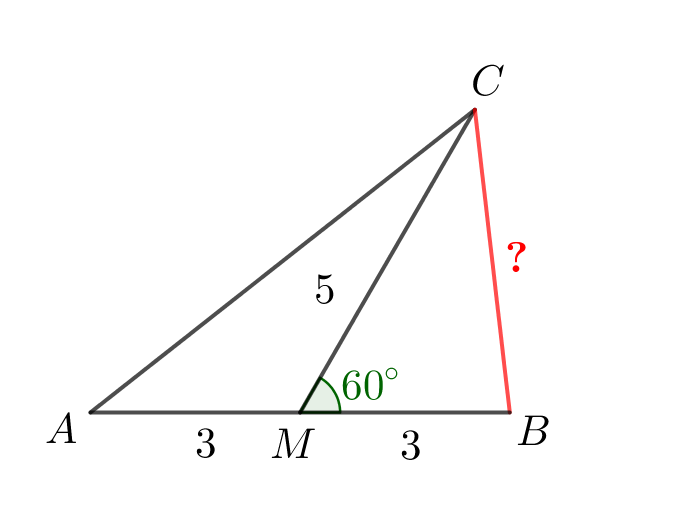 |
\(\displaystyle BC^2=CM^2+BM^2-2\cdot CM\cdot BM\cdot\cos \angle BMC\small.\)
Подставим известные значения:
\(\displaystyle BC^2=5^2+3^2-2\cdot 5\cdot3\cdot\cos60^{\circ}\small,\)
\(\displaystyle BC^2=25+9-30\cdot\frac{1}{2}\small,\)
\(\displaystyle BC^2=19\small,\)
\(\displaystyle BC=\sqrt{19}\small.\)
Ответ: \(\displaystyle BC=\sqrt{19}\small.\)