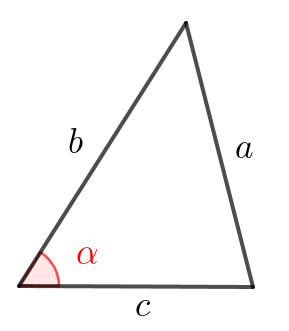
Стороны треугольника равны \(\displaystyle a,\,b,\,c\small.\) Найдите квадрат медианы, проведенной к стороне \(\displaystyle c{\small:}\)
(В ответе укажите выражение, зависящее от \(\displaystyle a,\,b,\,c\small.\))
Поскольку \(\displaystyle m_c\) медиана, то \(\displaystyle AM=BM=\frac{c}{2}\small.\) Обозначим \(\displaystyle \angle AMC\) за \(\displaystyle \alpha\small.\) Тогда дополняющий его до развернутого угол \(\displaystyle \angle BMC=180^{\circ}-\alpha\small.\) | 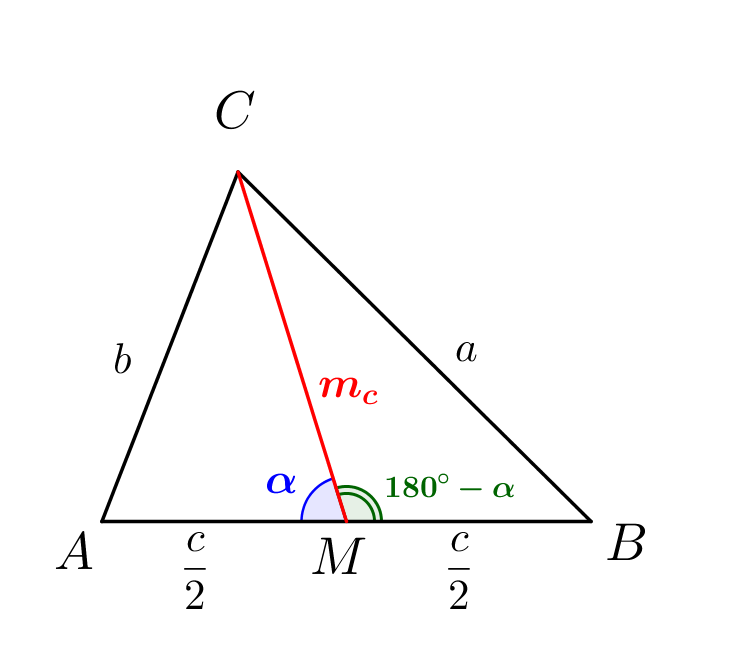 |
Для треугольника \(\displaystyle ACM\) получаем:
\(\displaystyle \color{blue}{b^2=m_c^2+\left(\frac{c}{2}\right)^2-2m_c\left(\frac{c}{2}\right)\cos\alpha}\small.\)
Для треугольника \(\displaystyle BCM\) получаем:
\(\displaystyle \color{green}{a^2=m_c^2+\left(\frac{c}{2}\right)^2-2m_c\left(\frac{c}{2}\right)\cos(180^{\circ}-\alpha)}\small.\)
Сложим выражения, полученные с помощью теоремы косинусов:
\(\displaystyle \color{blue}{b^2}+\color{green}{a^2}=\color{blue}{m_c^2+\left(\frac{c}{2}\right)^2-}\cancel{\color{blue}{2m_c\left(\frac{c}{2}\right)\cos\alpha}}+\color{green}{m_c^2+\left(\frac{c}{2}\right)^2-}\cancel{\color{green}{2m_c\left(\frac{c}{2}\right)\cos(180^{\circ}-\alpha)}}\small,\)
\(\displaystyle a^2+b^2=2m_c^2+2\left(\frac{c}{2}\right)^2\small.\)
Выразим \(\displaystyle m_c^2\) через \(\displaystyle a,\,b\) и \(\displaystyle c{\small:}\)
\(\displaystyle 2m_c^2=a^2+b^2-2\left(\frac{c}{2}\right)^2\small,\)
\(\displaystyle 2m_c^2=\frac{2a^2+2b^2-c^2}{2}\small,\)
\(\displaystyle m_c^2=\frac{2a^2+2b^2-c^2}{4}\small.\)
Ответ: \(\displaystyle m_c^2=\frac{2a^2+2b^2-c^2}{4}\small.\)