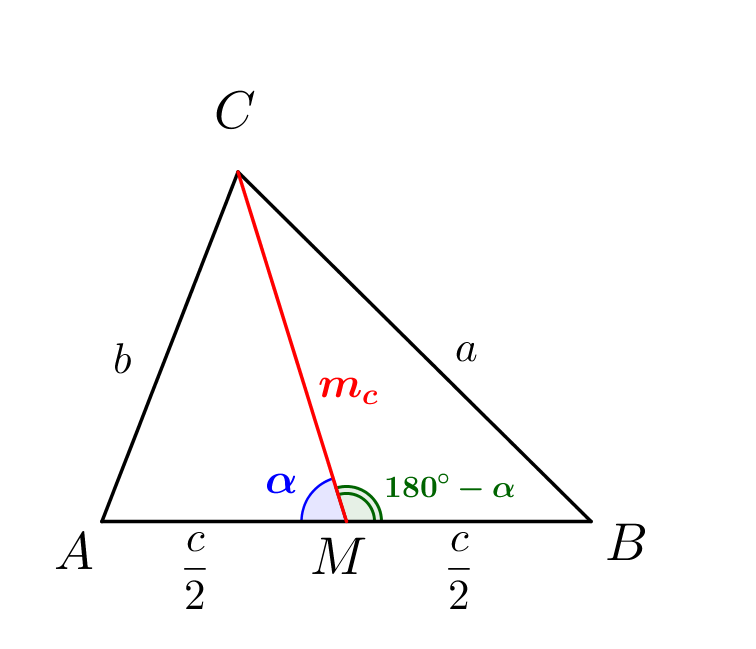
Найдите отношение суммы квадратов медиан треугольника к сумме квадратов его сторон:
\(\displaystyle m_c^2=\frac{2a^2+2b^2-c^2}{4}\small.\)
Тогда:
- длина медианы, проведенной к стороне \(\displaystyle a\small,\) равна:
\(\displaystyle m_a^2=\frac{2b^2+2c^2-a^2}{4}\small,\)
- длина медианы, проведенной к стороне \(\displaystyle b\small,\) равна:
\(\displaystyle m_b^2=\frac{2a^2+2c^2-b^2}{4}\small,\)
- длина медианы, проведенной к стороне \(\displaystyle c\small,\) равна:
\(\displaystyle m_c^2=\frac{2a^2+2b^2-c^2}{4}\small.\)
Выразим сумму квадратов медиан через квадраты сторон:
\(\displaystyle \begin{aligned}m_a^2+m_b^2+m_c^2&=\frac{2b^2+2c^2-a^2}{4}+\frac{2a^2+2c^2-b^2}{4}+\frac{2a^2+2b^2-c^2}{4}=\\[10px]&=\frac{3a^2+3b^2+3c^2}{4}=\frac{3}{4}(a^2+b^2+c^2)\small.\end{aligned}\)
Тогда отношение суммы квадратов медиан к сумме квадратов его сторон:
\(\displaystyle \left(\frac{3}{4}(a^2+b^2+c^2)\right):(a^2+b^2+c^2)=\frac{3}{4}\small.\)
Ответ: \(\displaystyle \frac{3}{4}\small.\)