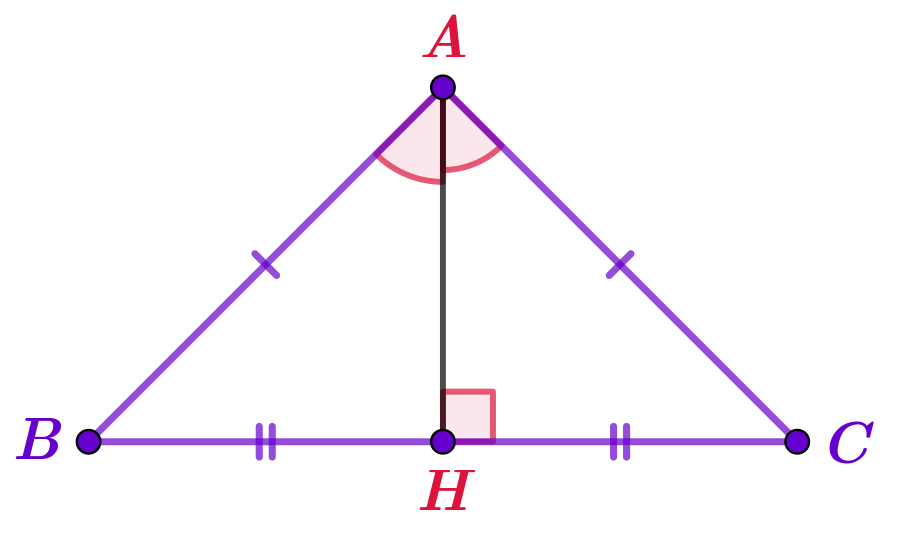
Периметр равнобедренного треугольника \(\displaystyle ABC\) равен \(\displaystyle 36\,{\footnotesize см}{\small .}\)
Высота \(\displaystyle CH{\small ,}\) опущенная на основание \(\displaystyle AB{\small ,}\) составляет \(\displaystyle 12\,{\footnotesize см}{\small .}\)
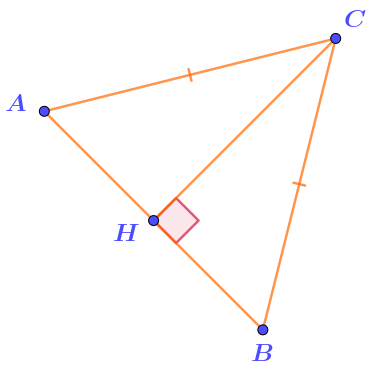
Найти периметр треугольника \(\displaystyle ACH{\small .}\)
\(\displaystyle P_{ACH}=\) \(\displaystyle {\footnotesize см}\)
Треугольник \(\displaystyle ABC\) равнобедренный по определению.
Отметим на рисунке соответствующие равные отрезки \(\displaystyle AH\) и \(\displaystyle BH{\small .}\)
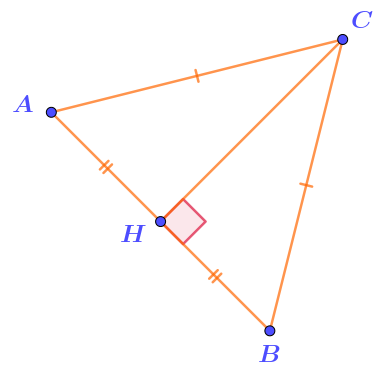
Периметр треугольника \(\displaystyle ACH-\)это сумма длин трёх его сторон. Одна из сторон известна: \(\displaystyle CH=12{\small .}\)
Не хватает длин двух других сторон \(\displaystyle AC\) и \(\displaystyle AH{\small .}\)
По условию, периметр треугольника \(\displaystyle ABC\) равен \(\displaystyle 36\,{\footnotesize (см)}\).
Он может быть представлен как сумма длин четырёх отрезков:
\(\displaystyle P_{ABC}=AC+AH+BC+BH{\small .}\)
Учитывая попарное равенство отрезков \(\displaystyle AC=BC{\small ,}\;\;AH=BH{\small ,}\) сумма длин отрезков \(\displaystyle AC\) и \(\displaystyle AH\) равна половине периметра треугольника \(\displaystyle ABC{\small :}\)
\(\displaystyle AC+AH=\frac{P_{ABC}}{2}=\frac{36}{2}=18\;{\footnotesize (см)}\)
Зная, что \(\displaystyle AC+AH=18\;{\footnotesize (см)}\) и \(\displaystyle CH=12\;{\footnotesize (см)}{\small ,}\) сложим эти два равенства, чтобы получить ответ на вопрос задачи:
\(\displaystyle P_{ACH}=AC+AH+CH=30\,{\footnotesize (см)}\)
Ответ: \(\displaystyle 30\,{\footnotesize см.}\)