Skip to main content

Теория: Свойства равнобедренного треугольника (короткая версия)

Задание

Перпендикулярные прямые \(\displaystyle a\) и \(\displaystyle b\) пересекаются в точке \(\displaystyle O{\small .}\)

Точка \(\displaystyle K\) одной из них одинаково удалена от двух точек \(\displaystyle A\) и \(\displaystyle B\) другой.

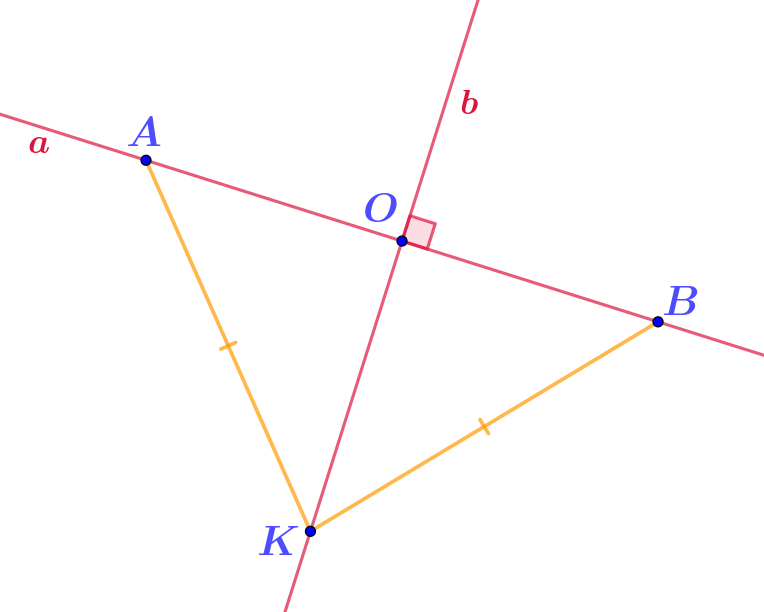
Дополните доказательство равенства отрезков \(\displaystyle OA\) и \(\displaystyle OB{\small .}\)
 

\(\displaystyle \left\{ \begin{array}{ll} \\ \\\\ \\ \end{array} \right.\)

 Перетащите сюда правильный ответ     
\(\displaystyle KO\) – высота
\(\displaystyle \triangle KAB\)		\(\displaystyle {\LARGE\Rightarrow}\) Перетащите сюда правильный ответ \(\displaystyle {\LARGE\Rightarrow}\)\(\displaystyle OA=OB\)
 (по свойству  равнобедренного треугольника)  

 

 

 

 

 

Решение

В треугольнике \(\displaystyle KAB\) стороны \(\displaystyle KA\) и \(\displaystyle KB\) равны, значит, этот треугольник – равнобедренный.

По условию,

\(\displaystyle a \perp b\) \(\displaystyle {\LARGE\Rightarrow}\) \(\displaystyle KO \perp AB{\small .}\)

Значит, \(\displaystyle KO\) – высота равнобедренного треугольника \(\displaystyle KAB{\small .}\)

Тогда \(\displaystyle KO\)– также медиана треугольника \(\displaystyle KAB\) по свойству равнобедренного треугольника.


Таким образом, дополнить доказательство равенства отрезков \(\displaystyle OA\) и \(\displaystyle OB\) нужно так:

 

\(\displaystyle \begin{cases}\\\\\\\end{cases} \)

\(\displaystyle KA=KB\)\(\displaystyle {\LARGE\Rightarrow}\)\(\displaystyle KO\) – медиана \(\displaystyle {\vartriangle}KAB\)

(по свойству  равнобедренного треугольника)

\(\displaystyle {\LARGE\Rightarrow}\)\(\displaystyle OA=OB\)
\(\displaystyle KO\) – высота\(\displaystyle {\vartriangle}KAB\)