На сторонах двух углов с общей стороной от вершины отложили равные отрезки \(\displaystyle OA=OB=OC{\small .}\)
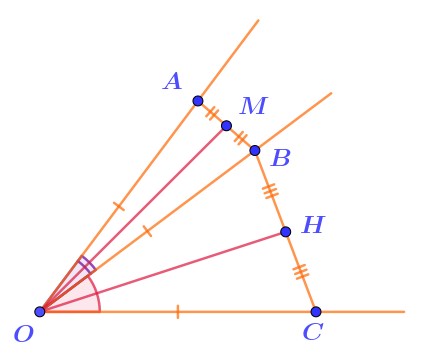
Найдите угол \(\displaystyle MOH\) между медианами треугольников \(\displaystyle AOB\) и \(\displaystyle BOC\), если известно, что
\(\displaystyle \angle AOB=16\degree {\small ,\;}\angle BOC=36\degree {\small .}\)
\(\displaystyle \angle MOH=\)\(\displaystyle \degree {\small .}\)
Найдём величину угла, складывая меры его частей \(\displaystyle -\) углов \(\displaystyle BOM\) и \(\displaystyle BOH{\small .}\)
В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к его основанию, совпадают.
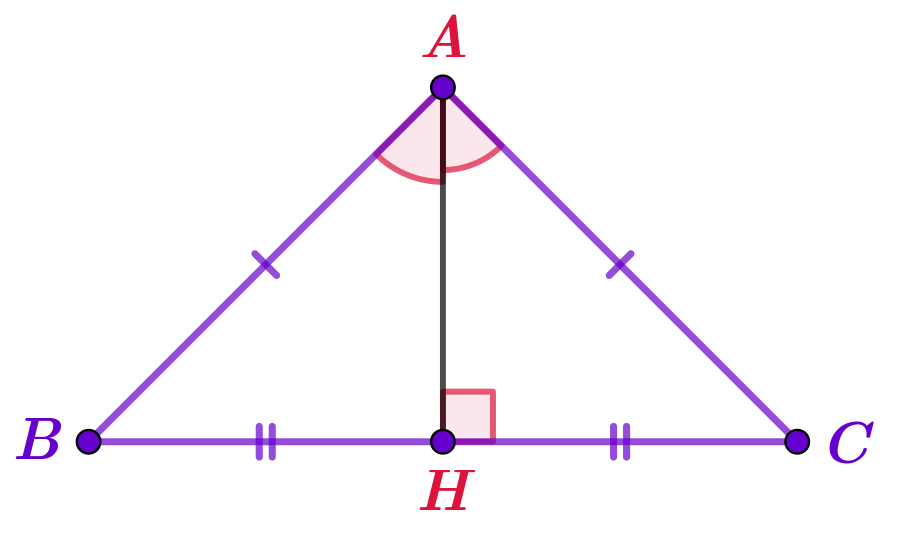
На рисунке отрезок \(\displaystyle AH\)– медиана, биссектриса и высота треугольника \(\displaystyle ABC{\small .}\)
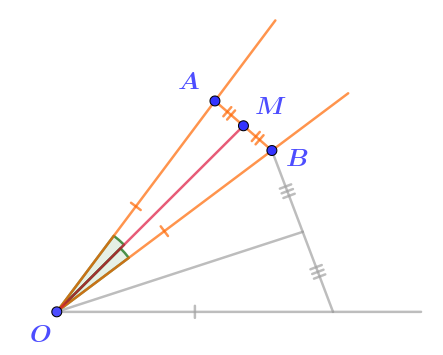
Треугольник \(\displaystyle AOB\)– равнобедренный по определению, \(\displaystyle OM\)– медиана, проведённая к основанию \(\displaystyle AB{\small .}\)
По свойству, \(\displaystyle OM\)– биссектриса треугольника \(\displaystyle AOB\), тогда
\(\displaystyle \angle BOM = \frac {\,\,16\degree}{2}=8\degree{\small .}\)
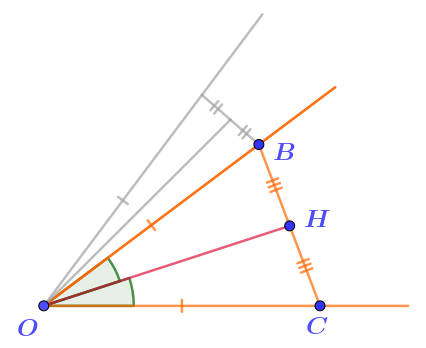
Треугольник \(\displaystyle BOC\) равнобедренный, \(\displaystyle OH\)– медиана, проведённая к основанию \(\displaystyle BC{\small .}\)
По свойству, \(\displaystyle OH\)– биссектриса треугольника \(\displaystyle BOC\), тогда
\(\displaystyle \angle BOH= \frac {\,\,36\degree}{2}=18\degree{\small .}\)

Градусная мера угла \(\displaystyle MOH\) равна сумме величин его частей:
\(\displaystyle \angle MOH=\angle BOM+\angle BOH=8\degree +18\degree=26\degree{\small .}\)
Ответ: \(\displaystyle 26\degree{\small .}\)