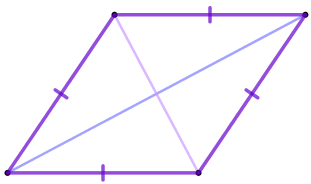
Точка \(\displaystyle O\) – точка пересечения диагоналей ромба \(\displaystyle ABCD{\small,}\) угол \(\displaystyle ABO\) равен \(\displaystyle 64^{\circ}{\small.}\) Найдите угол \(\displaystyle BAO{\small.}\) Ответ дайте в градусах.
\(\displaystyle \angle BAO=\)\(\displaystyle ^{\circ}{\small.}\)
Требуется найти угол \(\displaystyle BAO{\small.}\) | 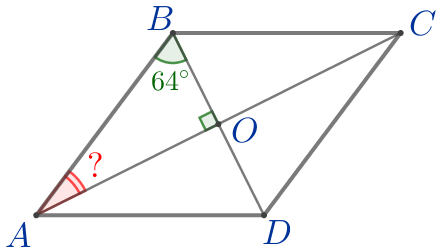 |
Воспользуемся одним из свойств ромба.
| Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. | 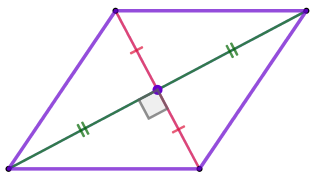 |
Значит, \(\displaystyle \angle AOB=90^{\circ}{\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle BAO{\small.}\)
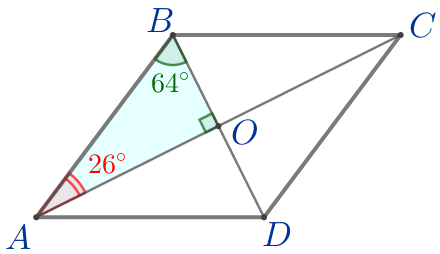
| В прямоугольном треугольнике сумма острых углов равна \(\displaystyle 90^{\circ}{\small.}\) Тогда \(\displaystyle \angle BAO = 90^{\circ}-\angle ABO=90^{\circ}-64^{\circ}=26^{\circ}.\) |
Ответ: \(\displaystyle \angle BAO=26^{\circ} {\small .}\)