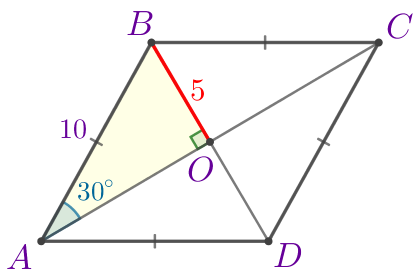
Теория: Признаки и свойства. Перпендикулярность диагоналей

Задание

Сторона ромба \(\displaystyle ABCD\) равна \(\displaystyle 10{\small,}\) \(\displaystyle O\) – точка пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD\) данного ромба. Найдите длину отрезка \(\displaystyle BO{\small,}\) если \(\displaystyle \angle BAO=30^{\circ}.\)

\(\displaystyle BO=\)

Решение

\(\displaystyle ABCD\) – ромб.

\(\displaystyle AB=10{\small;}\)
\(\displaystyle AC\) и \(\displaystyle BD\) – диагонали ромба;
\(\displaystyle O\) – точка пересечения диагоналей ромба;
\(\displaystyle \angle BAO=30^{\circ}{\small.}\)

Требуется найти длину отрезка \(\displaystyle BO{\small.}\)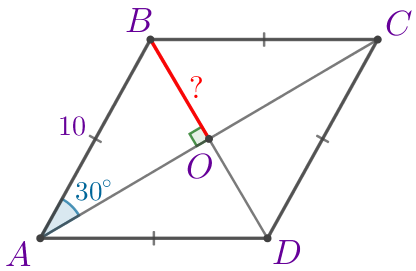

Воспользуемся одним из свойств ромба.

Свойство диагоналей ромба

Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.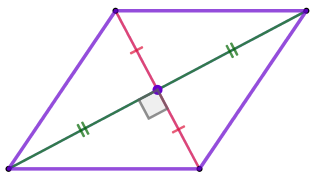

Значит, \(\displaystyle \angle AOB=90^{\circ}{\small.}\)

Рассмотрим прямоугольный треугольник \(\displaystyle AOB{\small.}\)

В прямоугольном треугольнике напротив угла \(\displaystyle 30^{\circ}\) лежит катет, равный половине гипотенузы. Значит,

\(\displaystyle BO=\frac{1}{2}\cdot AB=\frac{1}{2}\cdot 10=5 {\small.}\)

Ответ: \(\displaystyle BO=5 {\small .}\)