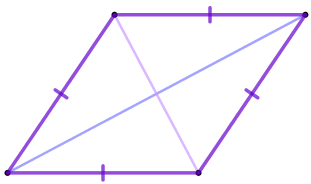
Точка \(\displaystyle O\) – точка пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD\) ромба \(\displaystyle ABCD{\small,}\) биссектрисы \(\displaystyle AK\) и \(\displaystyle BN\) треугольника \(\displaystyle ABO\) пересекаются в точке \(\displaystyle L{\small.}\) Найдите угол \(\displaystyle ALB{\small.}\) Ответ дайте в градусах.
\(\displaystyle \angle ALB=\)\(\displaystyle ^{\circ}{\small.}\)
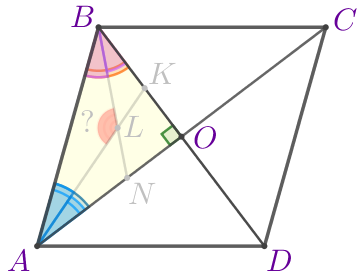
По условию задачи выполним построение.
Требуется найти угол \(\displaystyle ALB{\small.}\) | 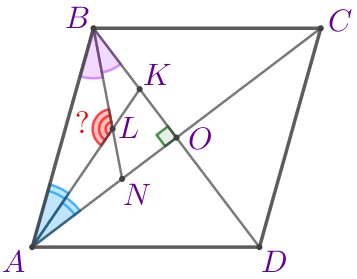 |
Воспользуемся одним из свойств ромба.
| Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. | 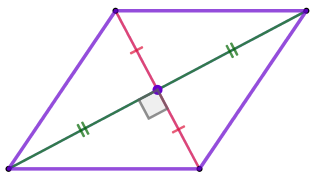 |
Значит, \(\displaystyle \angle AOB=90^{\circ}{\small.}\)
Рассмотрим прямоугольный треугольник \(\displaystyle AOB{\small.}\)
| Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle BAO+\angle ABO=90^{\circ}{\small.}\) |
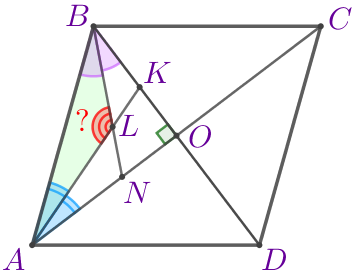
Рассмотрим треугольник \(\displaystyle ALB{\small.}\)
| Так как сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small,}\) то \(\displaystyle \angle ALB=180^{\circ}-(\angle BAL+\angle ABL){\small.}\)
|
Тогда
\(\displaystyle \angle BAL+\angle ABL=\frac{1}{2}\bigg(\angle BAO+\angle ABO\bigg)=\frac{1}{2} \cdot 90^{\circ}=45^{\circ}{\small.}\)
Следовательно,
\(\displaystyle \angle ALB=180^{\circ}-(\angle BAL+\angle ABL)=180^{\circ}-45^{\circ}=135^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle ALB=135^{\circ}{\small.}\)