На отрезке \(\displaystyle PS\) длиной \(\displaystyle 104\) отмечены точки \(\displaystyle Q\) и \(\displaystyle R{\small ,}\) как показано на чертеже.
Известны длины отрезков:
\(\displaystyle PR=77\) и \(\displaystyle QS=63{\small .}\)
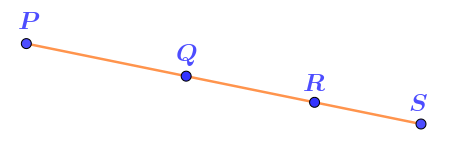
Найти длину отрезка \(\displaystyle QR{\small .}\)
\(\displaystyle QR=\)
Распишем известные длины отрезков в виде сумм длин частей:
\(\displaystyle PR=PQ+QR=77;\;\;\;\;\;\;QS=QR+RS=63{\small .}\)
Почленно сложив записанные равенства, получим:
\(\displaystyle PQ+QR+QR+RS=140{\small .}\)
Поэтому три слагаемых в полученной сумме можно заменить на длину отрезка \(\displaystyle SP{\small :}\)
\(\displaystyle QR+104=140{\small .}\)
Из этого равенства выражаем длину отрезка \(\displaystyle QR{\small :}\)
\(\displaystyle QR=140-104=36{\small .}\)
Ответ: \(\displaystyle 36{\small .}\)