На клетчатой бумаге со стороной клетки \(\displaystyle 12~{\footnotesize мм}\) начерчен четырёхугольник.
На одной из его сторон поставили точку \(\displaystyle P{\small .}\)
При этом образовались отмеченные равные отрезки.
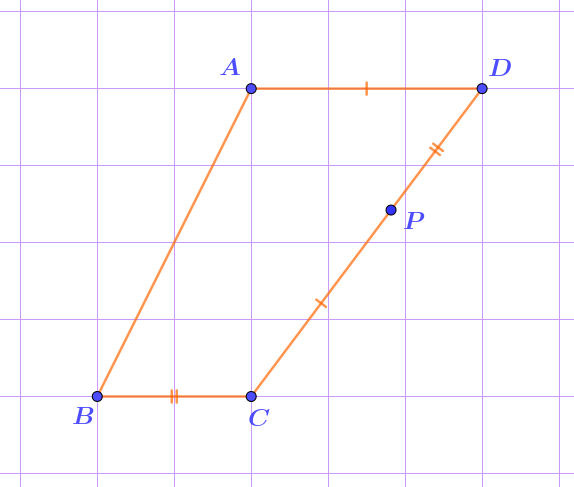
Определите, сколько сантиметров составляет длина стороны \(\displaystyle CD{\small .}\)
\(\displaystyle CD=\)см
Длины отрезков \(\displaystyle DP\) и \(\displaystyle CP\) соответственно равны длинам равных им отрезков \(\displaystyle BC\) и \(\displaystyle AD{\small .}\)
Эти отрезки имеют длины \(\displaystyle 2\) и \(\displaystyle 3\) клетки.
Значит:
\(\displaystyle CD=2+3=5~\)клеток.
Поскольку в одном сантиметре содержится \(\displaystyle 10\) миллиметров, длина стороны клетки составляет \(\displaystyle \frac{12}{10}=1{,}2~{\footnotesize см}{\small .}\)
Таким образом:
\(\displaystyle CD=5\cdot 1{,}2=6~({\footnotesize см}){\small .}\)
Ответ: \(\displaystyle 6~{\footnotesize см}{\small .}\)