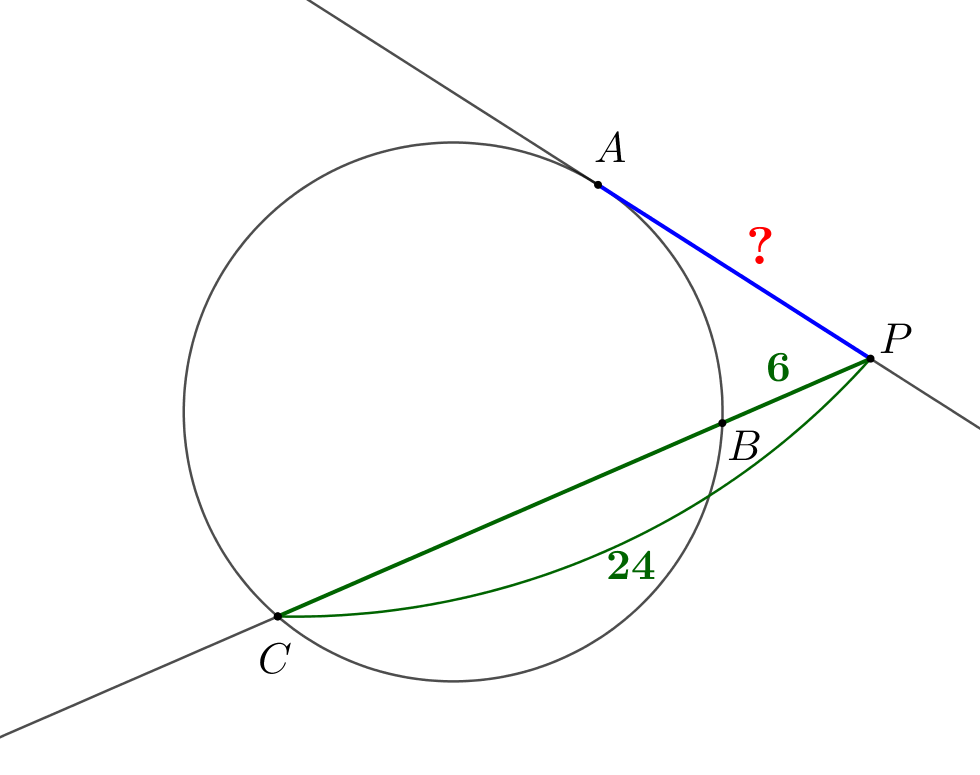
Точка \(\displaystyle P\) лежит вне окружности. Через точку \(\displaystyle P\) провели прямую, касающуюся окружности в точке \(\displaystyle A\small,\) и луч, пересекающий окружность в точках \(\displaystyle B\) и \(\displaystyle C\small.\) Найдите \(\displaystyle AP\small,\) если \(\displaystyle PB=6\) и \(\displaystyle PC=24\small.\)
Угол между хордой и касательной равен вписанному углу, опирающемуся на данную хорду: \(\displaystyle \angle PAB=\angle BCA\small.\)
Тогда треугольники \(\displaystyle APC\) и \(\displaystyle BPA\) подобны по двум углам. Значит, выполняется равенство: \(\displaystyle \frac{AP}{CP}=\frac{BP}{AP}\small.\) | 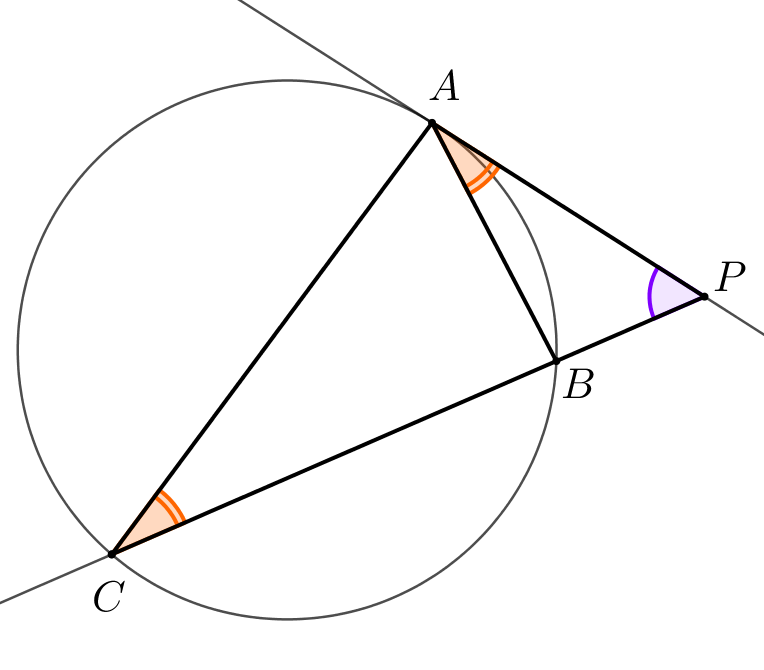 |
Тогда
\(\displaystyle AP^2=BP\cdot CP\small.\)
Подставляя известные значения \(\displaystyle BP=6,\,CP=24\small,\) получаем:
\(\displaystyle AP^2=6\cdot24\small,\)
\(\displaystyle AP=\sqrt{6\cdot24}=12\small.\)
Ответ: \(\displaystyle AP=12\small.\)
В ходе решения получили правило:
Теорема об отрезках касательной и секущей
Если секущая и касательная проведены к окружности из одной точки, то квадрат расстояния до точки касания равен произведению отрезков секущей:
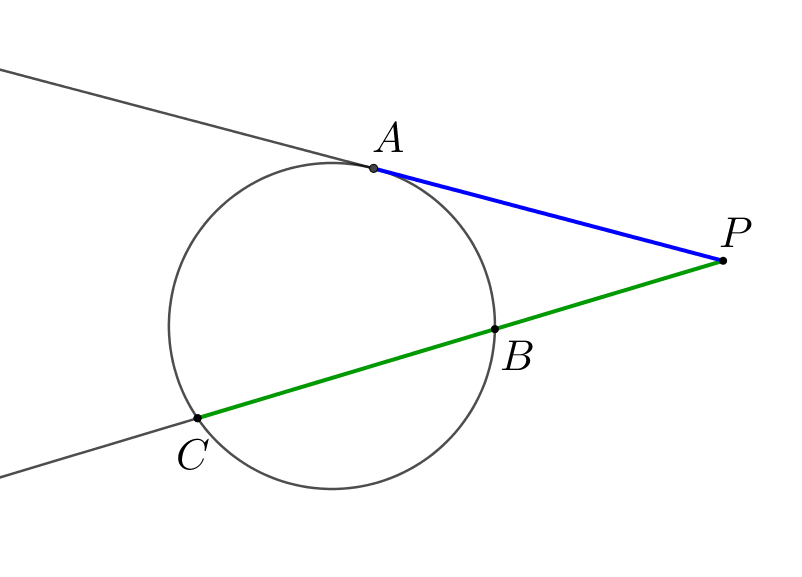
\(\displaystyle \color{blue}{AP^2}=\color{green}{BP}\cdot \color{green}{CP}\)