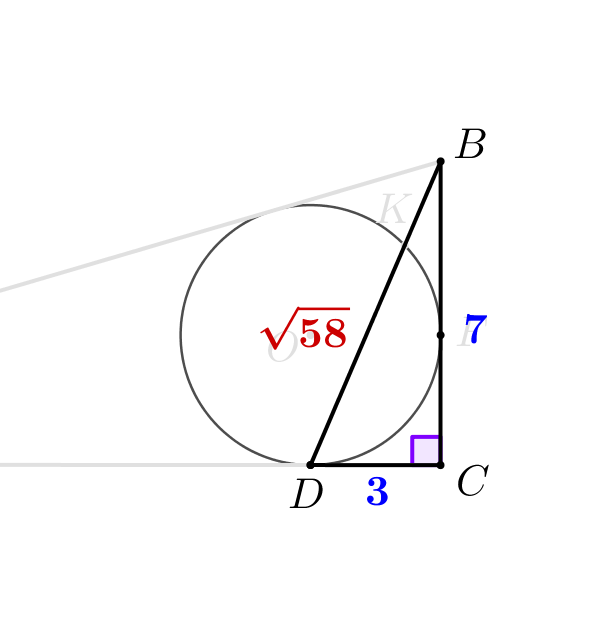
В прямоугольном треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) – прямой. Вписанная окружность треугольника \(\displaystyle ABC\) касается стороны \(\displaystyle AC\) в точке \(\displaystyle D\small.\) Известно, что \(\displaystyle BC=7\small,\) а радиус вписанной окружности равен \(\displaystyle r=3\small.\) Найдите длину хорды, соединяющей точки пересечения окружности с прямой \(\displaystyle BD\small.\)
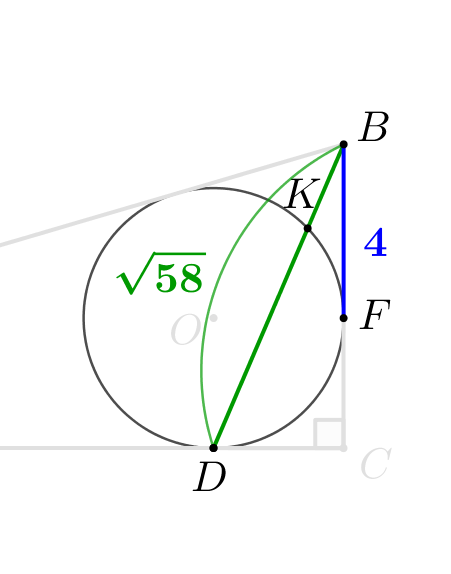
Точка \(\displaystyle O\) – центр вписанной окружности. Вписанная окружность касается стороны \(\displaystyle BC\) в точке \(\displaystyle F\small.\) Пересечение вписанной окружности и прямой \(\displaystyle BD\) – точка \(\displaystyle K\small.\) Необходимо найти \(\displaystyle KD\small.\) Тогда, чтобы решить задачу, найдем \(\displaystyle BD\) и \(\displaystyle BK\small.\) | 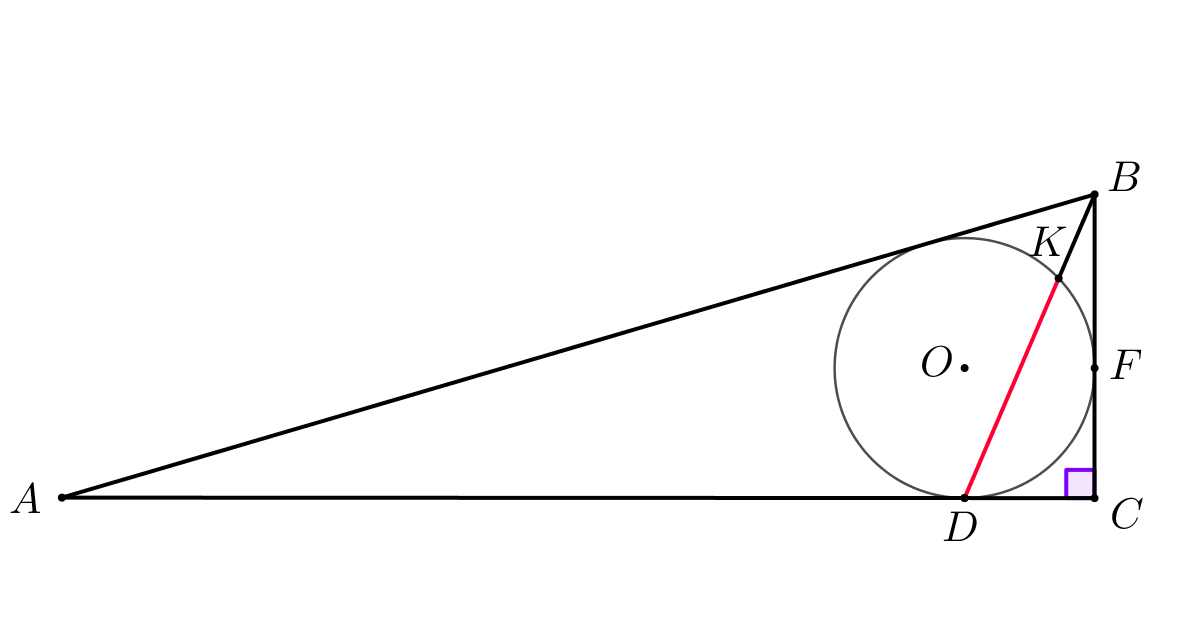 |
Проведем отрезки \(\displaystyle OD\) и \(\displaystyle OF\small.\) Поскольку радиус перпендикулярен касательной, то \(\displaystyle \angle CFO=\angle CDO=90^{\circ}\small.\) Тогда в четырехугольнике \(\displaystyle CDOF\) три прямых угла. Значит, это прямоугольник. При этом у этого четырехугольника две смежные стороны равны: \(\displaystyle OD=OF=r=3\small.\) Значит, это квадрат и \(\displaystyle OD=OF=CF=CD=3\small.\) | 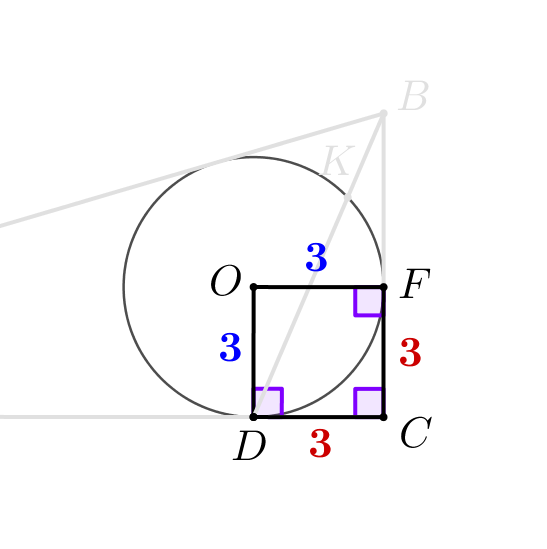 |
\(\displaystyle BD=\sqrt{58}\small.\)
\(\displaystyle BK=\frac{16}{\sqrt{58}}\small.\)
Тогда
\(\displaystyle KD=BD-BK=\sqrt{58}-\frac{16}{\sqrt{58}}=\frac{58-16}{\sqrt{58}}=\frac{42}{\sqrt{58}}=\frac{21\sqrt{58}}{29}\small.\)
Ответ: \(\displaystyle \frac{21\sqrt{58}}{29}\small.\)