Из точки \(\displaystyle A\small,\) лежащей вне окружности, проведены к окружности касательная и секущая. Расстояние от точки \(\displaystyle A\) до точки касания равно \(\displaystyle 16\small,\) а расстояние от точки \(\displaystyle A\) до одной из точек пересечения секущей с окружностью равно \(\displaystyle 32\small.\) Найдите радиус окружности, если расстояние от центра окружности до секущей равно \(\displaystyle 5\small.\)
Точка \(\displaystyle O\) – центр окружности. Пусть общая точка окружности и касательной – \(\displaystyle K\small.\) А секущая пересекает окружность в точках \(\displaystyle B\) и \(\displaystyle C\small.\) | 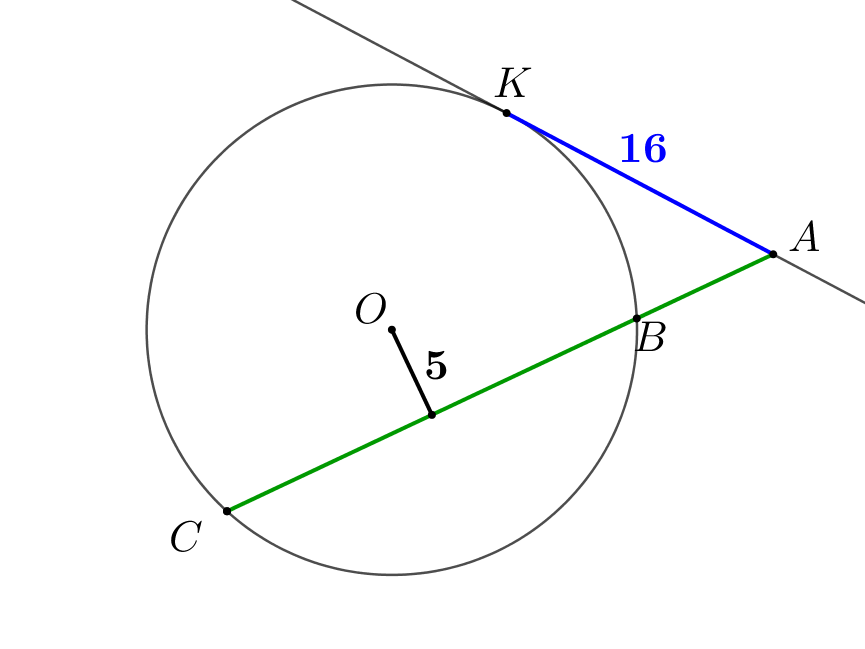 |
\(\displaystyle BC=24\)
Произведение отрезков секущей равно квадрату касательной. Тогда
\(\displaystyle AK^2=AB\cdot AC\small.\)
\(\displaystyle AK=16\small,\) а один из отрезков \(\displaystyle AB\) или \(\displaystyle AC\) равен \(\displaystyle 32\small,\) тогда второй равен
\(\displaystyle \frac{16^2}{32}=8\small.\)
Значит, \(\displaystyle AB=8\) и \(\displaystyle AC=32\small.\)
Тогда
\(\displaystyle BC=AC-AB=32-8=24\small.\)
\(\displaystyle BO=13\small.\)
Рассмотрим треугольник \(\displaystyle OBC\small.\) Он равнобедренный, так как \(\displaystyle OB=OC\small.\) Проведем в нем высоту \(\displaystyle OH\small.\) Поскольку треугольник равнобедренный, \(\displaystyle OH\) также является медианой: \(\displaystyle BH=CH=\frac{BC}{2}=12\small.\) По условию, расстояние от \(\displaystyle O\) до секущей равно \(\displaystyle 5\small.\) То есть \(\displaystyle OH=5\small.\) Тогда в прямоугольном треугольнике \(\displaystyle OBH\) катеты \(\displaystyle BH=12\) и \(\displaystyle OH=5\small.\) По теореме Пифагора находим гипотенузу: \(\displaystyle BO^2=OH^2+BH^2=5^2+12^2=169\small,\) \(\displaystyle BO=\sqrt{169}=13\small.\) | 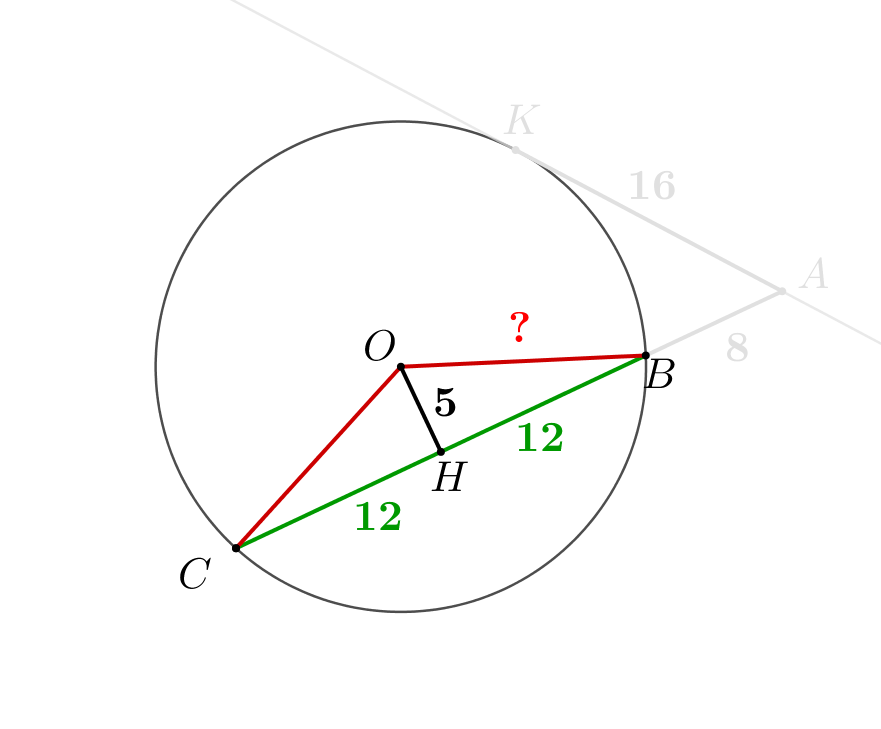 |
Ответ: \(\displaystyle 13\small.\)