Через вершину наибольшего угла треугольника со сторонами \(\displaystyle 3,\,4,\,5\) проведена касательная к окружности, описанной около этого треугольника. Найдите отрезок касательной, заключенный между точкой касания и точкой пересечения с продолжением наибольшей стороны треугольника.
В треугольнике против большей стороны лежит больший угол. Тогда касательную провели через вершину, лежащую напротив стороны \(\displaystyle 5\small.\)
Необходимо найти \(\displaystyle CD\small.\)
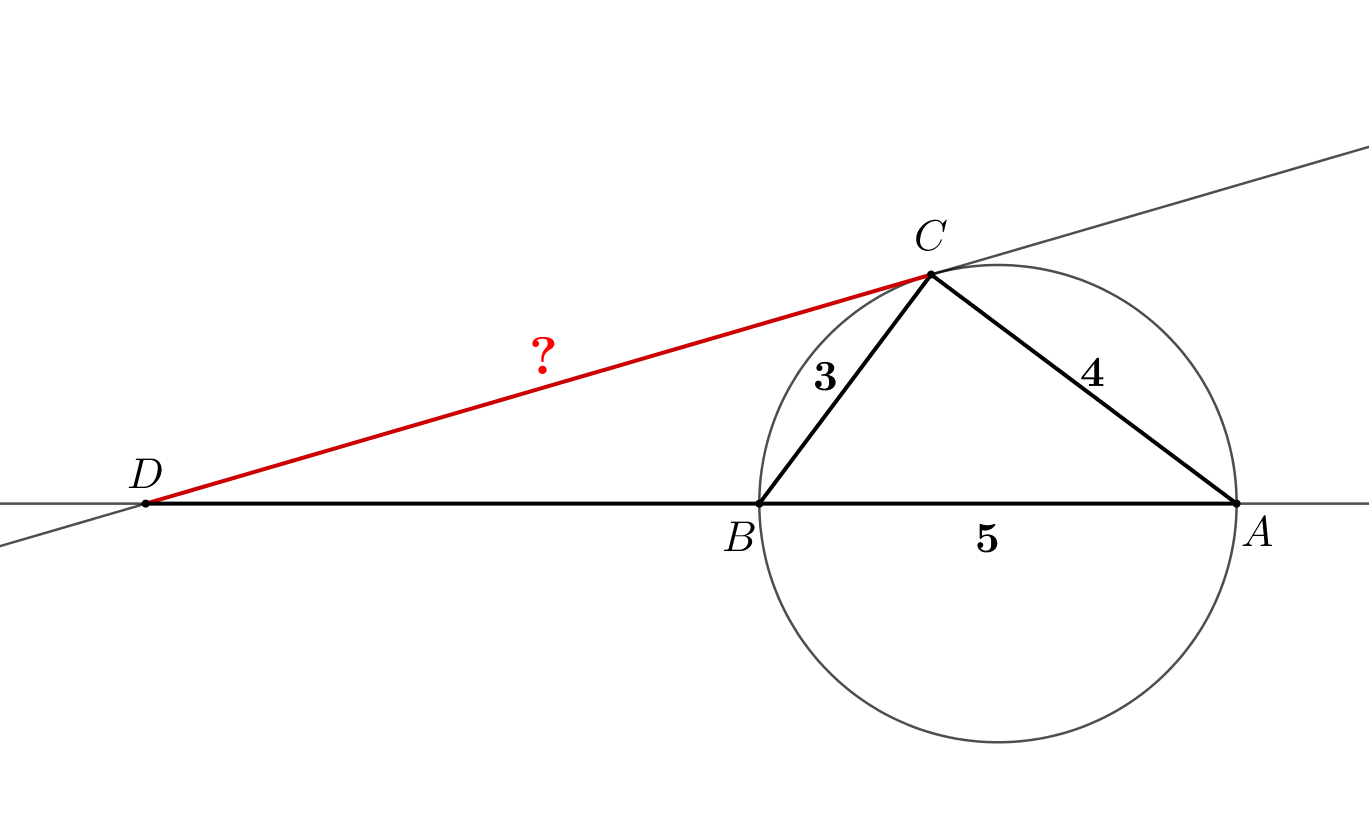
1. Произведение отрезков секущей равно квадрату касательной. Тогда \(\displaystyle CD^2=BD\cdot AD\small.\) Обозначим \(\displaystyle BD\) за \(\displaystyle x\) тогда \(\displaystyle CD^2=x\cdot (x+5)\small.\) | 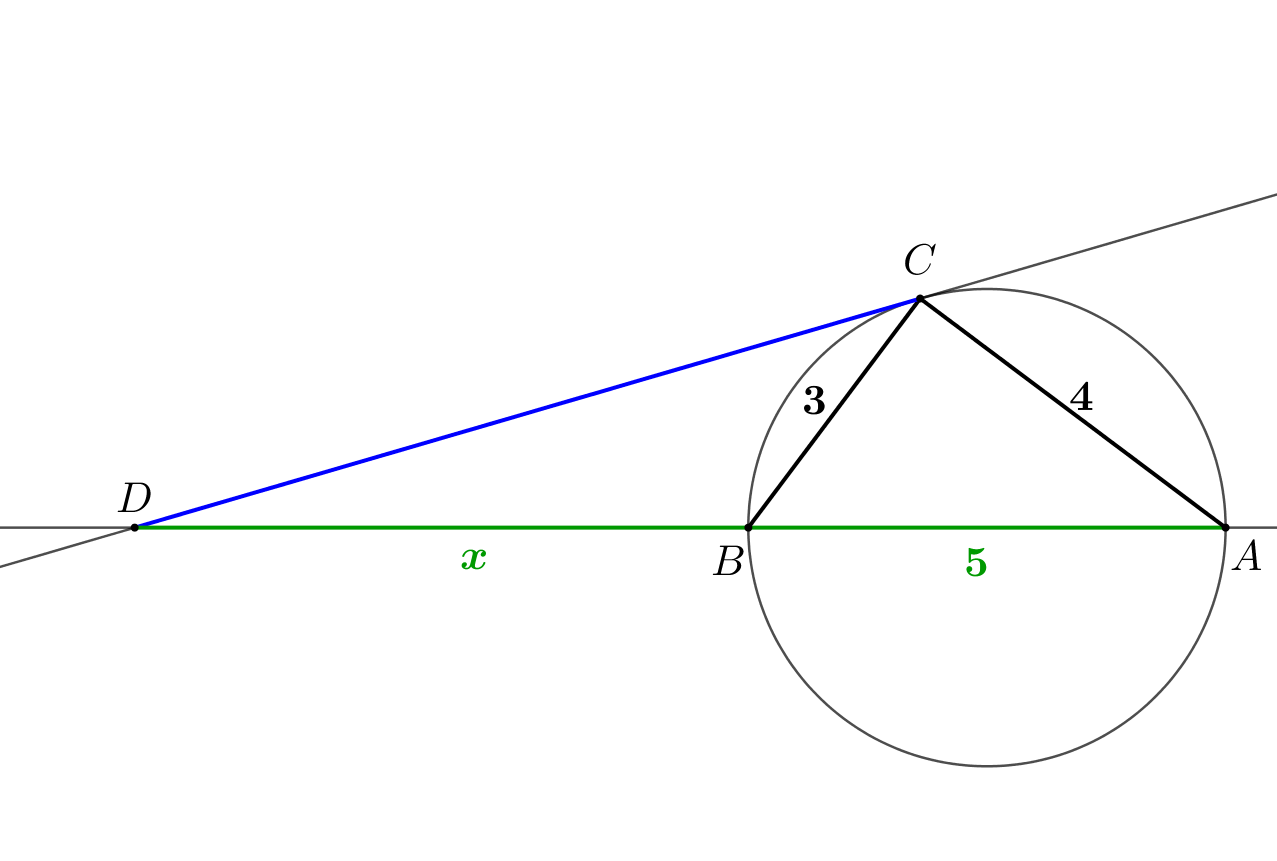 |
2. Установим еще одну зависимость между \(\displaystyle CD\) и \(\displaystyle x\small.\) Угол между хордой и касательной равен вписанному углу, опирающемуся на данную хорду: \(\displaystyle \angle DCB=\angle BAC\small.\) | 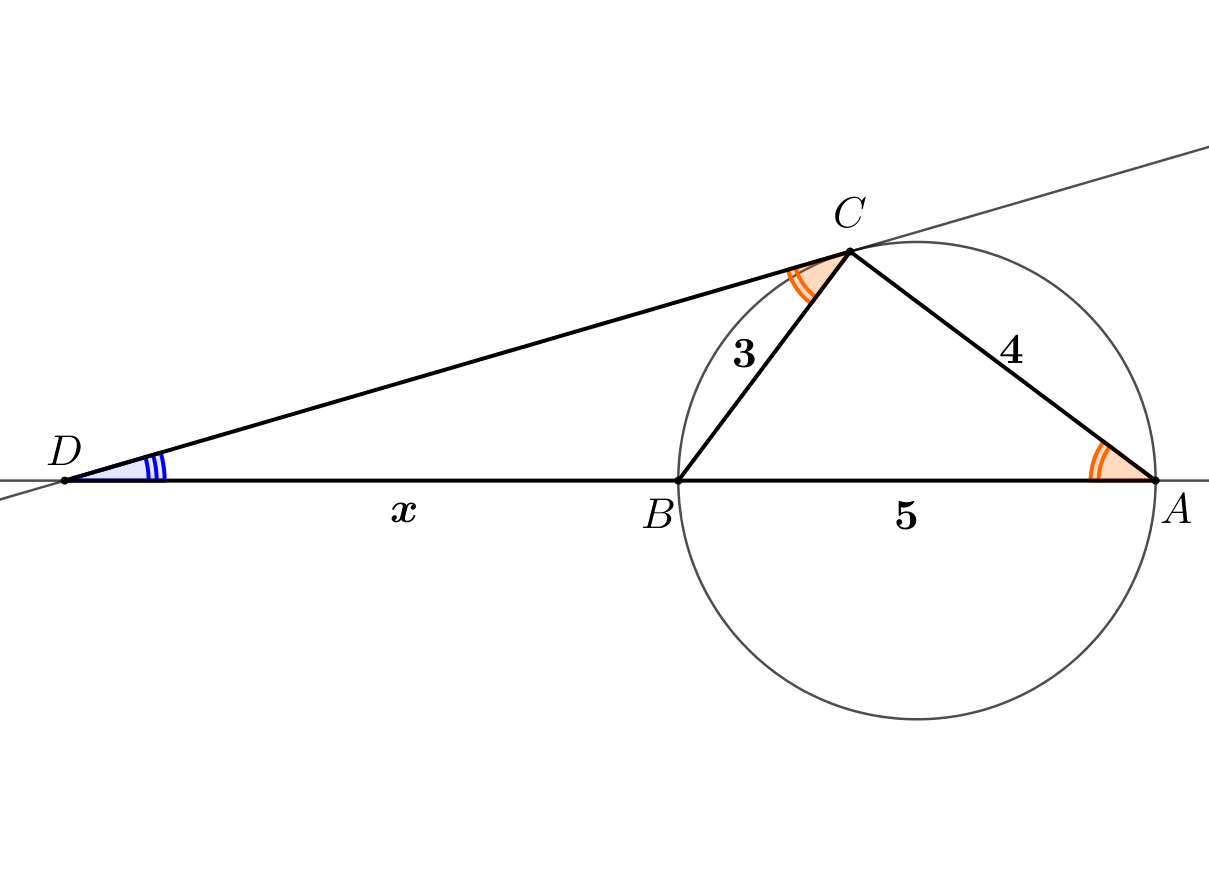 |
Тогда треугольники \(\displaystyle DCB\) и \(\displaystyle DAC\) подобны по двум углам. Тогда \(\displaystyle \frac{BD}{CD}=\frac{BC}{AC}\small.\) |
\(\displaystyle \frac{BD}{CD}=\frac{3}{4}\small.\)
То есть
\(\displaystyle CD=\frac{4\cdot BD}{3}=\frac{4x}{3}\small.\)
3. Используя, что \(\displaystyle CD=\frac{4x}{3}\small,\) получаем
\(\displaystyle x\cdot (x+5)=CD^2=\left(\frac{4x}{3}\right)^2\small.\)
\(\displaystyle x=\frac{45}{7}\small.\)
Тогда
\(\displaystyle CD=\frac{4x}{3}=\frac{4}{3}\cdot\frac{45}{7}=\frac{60}{7}\small.\)
Ответ: \(\displaystyle \frac{60}{7}\small.\)