Укажите верное утверждение.
Рассмотрим каждое утверждение:
верно
| Квадратом называется прямоугольник, у которого все стороны равны. | 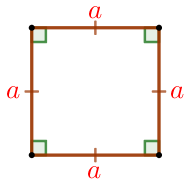 |
Согласно определению квадрата данное утверждение верно.
неверно
Утверждение является верным, если оно верно во всех случаях.
Однако не каждый параллелограмм с равными сторонами является квадратом. Например, ромб.
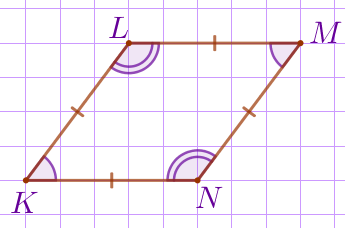 | \(\displaystyle \color{darkviolet}{KL}=\color{darkviolet}{LM}=\color{darkviolet}{MN}=\color{darkviolet}{KN}{\small,}\) \(\displaystyle \angle K \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle L \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle M \,\cancel=\, 90^{\circ}{\small,}\) \(\displaystyle \angle N \,\cancel=\, 90^{\circ}{\small.}\) \(\displaystyle KLMN\) – не квадрат. |
Следовательно, данное утверждение неверно.
неверно
Утверждение является верным, если оно верно во всех случаях.
Однако не каждый четырёхугольник, у которого все углы прямые, является квадратом. Например, прямоугольник с неравными смежными сторонами.
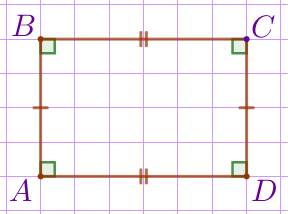 | \(\displaystyle \angle A =\angle B=\angle C=\angle D=90^{\circ}{\small,}\) \(\displaystyle \color{darkviolet}{AB}\, \cancel=\, \color{darkviolet}{BC}{\small.}\)
\(\displaystyle ABCD\) – не квадрат. |
Следовательно, данное утверждение неверно.
Ответ: Прямоугольник, у которого все стороны равны, является квадратом.