Задание
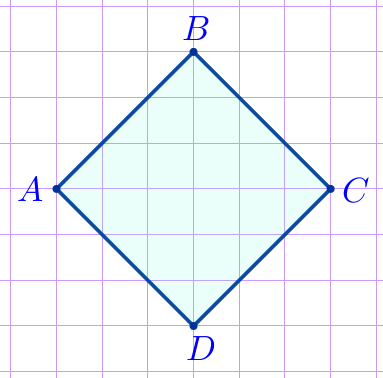
На клетчатой бумаге изображён четырёхугольник \(\displaystyle ABCD{\small.}\) Является ли данный четырёхугольник квадратом?
Решение
Определение
| Квадратом называется параллелограмм, у которого все стороны равны и все углы прямые. |  |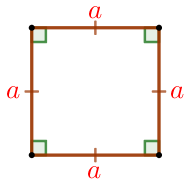
Рассмотрим четырёхугольник \(\displaystyle ABCD{\small.}\)
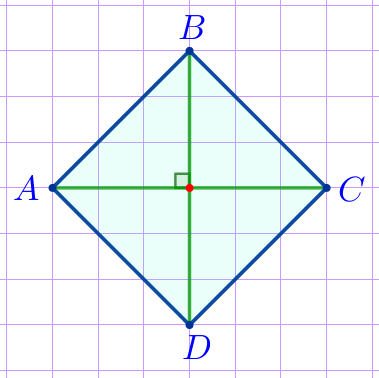
По рисунку видим:
Диагонали точкой пересечения делятся пополам. Значит,
\(\displaystyle ABCD\) – параллелограмм.
Диагонали перпендикулярны. Значит,
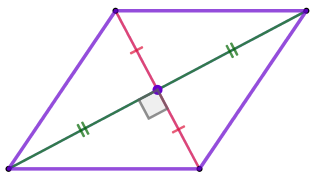
параллелограмм \(\displaystyle ABCD\) является ромбом, то есть
\(\displaystyle AB=BC=CD=AD{\small.}\)
Диагонали равны: \(\displaystyle AC=BD{\small.}\) Значит,
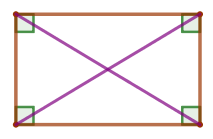
параллелограмм \(\displaystyle ABCD\) является прямоугольником, то есть
\(\displaystyle \angle A=\angle B=\angle C=\angle D=90^{\circ}{\small.}\)
В результате получаем
\(\displaystyle ABCD\) – это прямоугольник, у которого все стороны равны.
Значит,
данный четырёхугольник \(\displaystyle ABCD\) является квадратом.
Ответ: Да.
Замечание / комментарий
| Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом. | 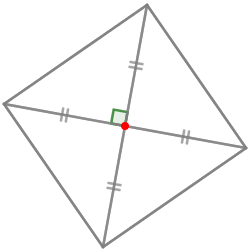 |