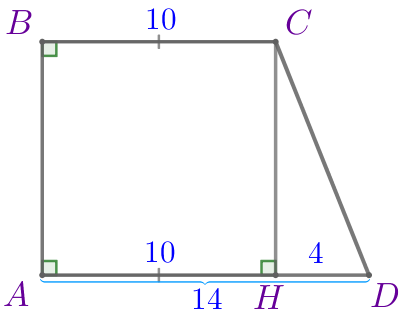
Высота \(\displaystyle CH{\small,}\) опущенная из вершины тупого угла на большее основание прямоугольной трапеции \(\displaystyle ABCD{\small,}\) делит его на отрезки \(\displaystyle AH=10\) и \(\displaystyle HD=4{\small.}\) Найдите среднюю линию этой трапеции.
\(\displaystyle ABCD\) – прямоугольная трапеция:
Требуется найти среднюю линию данной трапеции. | 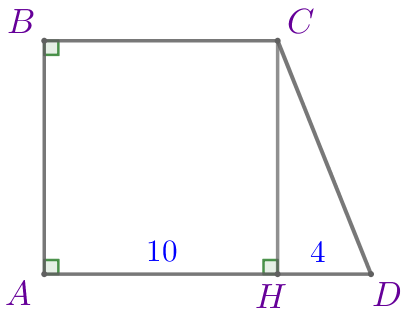 |
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 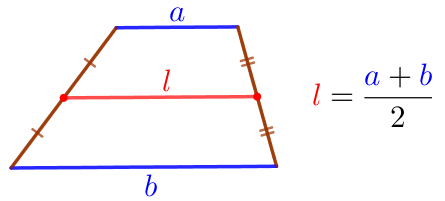 |
\(\displaystyle BC=10{\small;}\)
\(\displaystyle AD=14{\small.}\)
Длина средней линии трапеции \(\displaystyle ABCD\) равна
\(\displaystyle \frac{BC+AD}{2}=\frac{10+14}{2}=\frac{24}{2}=12{\small.}\)
Ответ: \(\displaystyle 12{\small .}\)