В трапеции \(\displaystyle ABCD\) с основаниями \(\displaystyle AD=16\) и \(\displaystyle BC=12\) провели среднюю линию \(\displaystyle MN{\small.}\) Найдите расстояние между серединами отрезков \(\displaystyle AM\) и \(\displaystyle ND{\small.}\)
\(\displaystyle ABCD\) – трапеция:
| 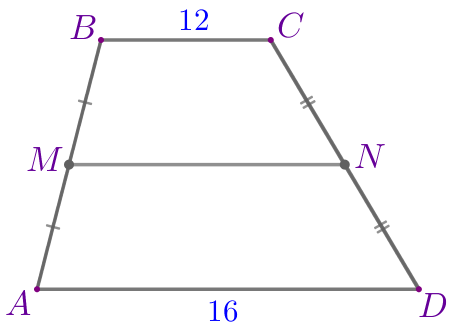 |
Требуется найти расстояние между серединами отрезков \(\displaystyle AM\) и \(\displaystyle ND{\small.}\)
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 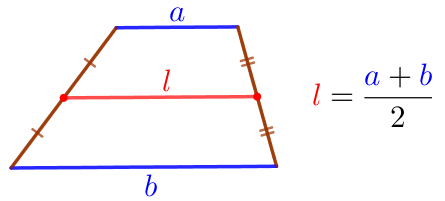 |
Так как средняя линия трапеции равна полусумме оснований, то
\(\displaystyle MN=\frac{AD+BC}{2}=\frac{16+12}{2}=\frac{28}{2}=14{\small.}\)
Рассмотрим четырехугольник \(\displaystyle AMND{\small.}\)
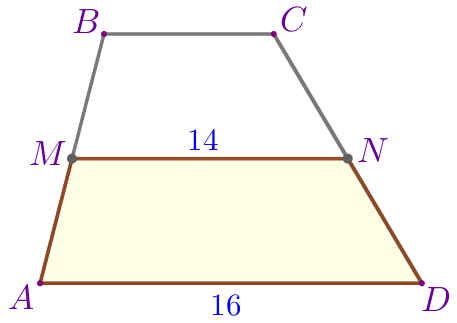 |
Значит, четырехугольник \(\displaystyle AMND\) является трапецией. |
| В задаче требуется найти расстояние между серединами отрезков \(\displaystyle AM\) и \(\displaystyle ND{\small,}\) то есть длину средней линии трапеции \(\displaystyle AMND{\small.}\) | 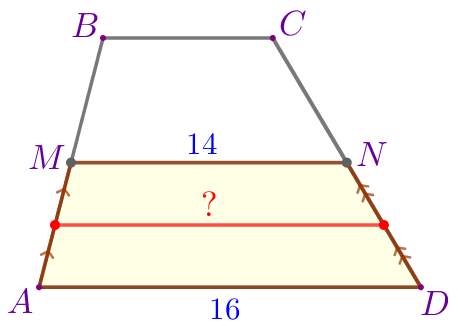 |
Средняя линия трапеции \(\displaystyle AMND\) равна полусумме оснований \(\displaystyle AD\) и \(\displaystyle MN{\small:}\)
\(\displaystyle \frac{AD+MN}{2}=\frac{16+14}{2}=\frac{30}{2}=15{\small.}\)
Ответ: \(\displaystyle 15{\small .}\)