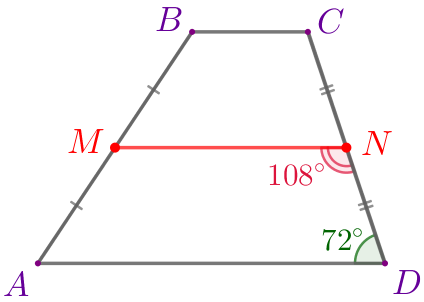
В трапеции \(\displaystyle ABCD\) угол \(\displaystyle D\) равен \(\displaystyle 72^{\circ}{\small,}\) точки \(\displaystyle M\) и \(\displaystyle N\) – середины боковых сторон \(\displaystyle AB\) и \(\displaystyle CD\) соответственно. Найдите угол \(\displaystyle MND{\small.}\) Ответ дайте в градусах.
\(\displaystyle ABCD\) – трапеция:
Требуется найти угол \(\displaystyle MND{\small.}\) | 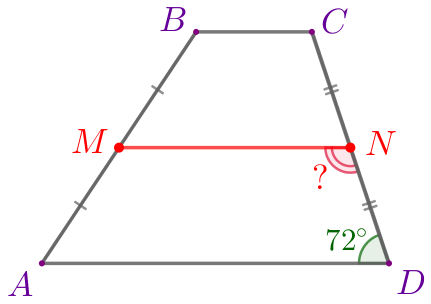 |
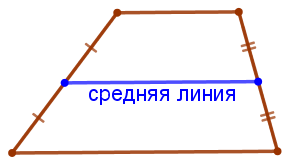
\(\displaystyle MN\) – средняя линия трапеции \(\displaystyle ABCD{\small.}\)
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 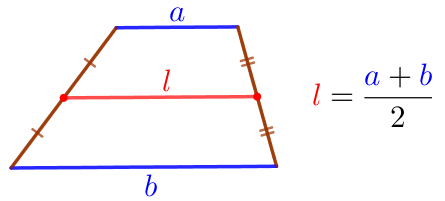 |
Значит,
\(\displaystyle MN\parallel BC\parallel AD{\small.}\)
Углы \(\displaystyle MND\) и \(\displaystyle ADC\) – односторонние при пересечении параллельных прямых \(\displaystyle MN\) и \(\displaystyle AD\) секущей \(\displaystyle CD\small.\)
| Сумма односторонних углов при пересечении параллельных прямых секущей равна \(\displaystyle 180^{\circ}{\small,}\) то есть \(\displaystyle \angle MND + \angle ADC=180^{\circ}{\small.}\) |
Значит,
\(\displaystyle \angle MND=180^{\circ}- \angle ADC=180^{\circ}-72^{\circ}=108^{\circ}{\small.}\)
Ответ: \(\displaystyle 108^{\circ}{\small .}\)