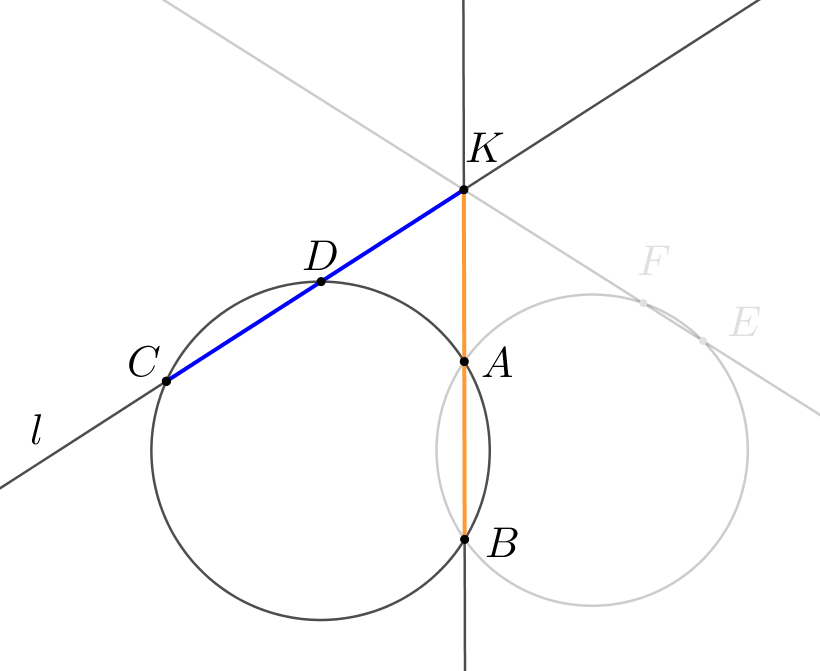
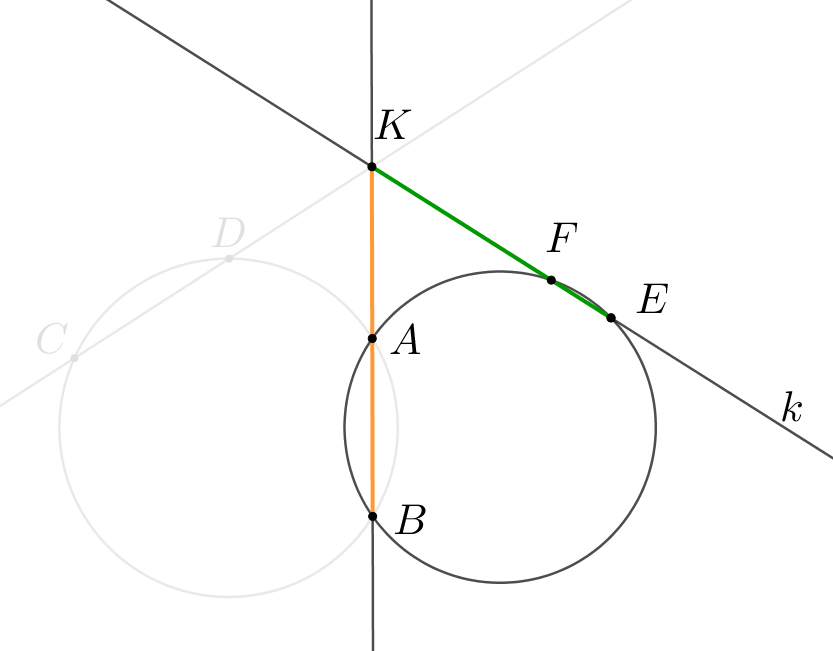
Две окружности пересекаются в точках \(\displaystyle A\) и \(\displaystyle B\small.\) На прямой \(\displaystyle AB\) выбрали точку \(\displaystyle K\small,\) лежащую вне окружностей и провели секущие \(\displaystyle l\) и \(\displaystyle k\small.\) Прямая \(\displaystyle l\) пересекает первую окружность в точках \(\displaystyle C\) и \(\displaystyle D\small,\) прямая \(\displaystyle k\) пересекает вторую окружность в точках \(\displaystyle E\) и \(\displaystyle F\small.\) Найдите \(\displaystyle KD\small,\) если \(\displaystyle KC=25,\,KE=20,\,KF=15\small.\)
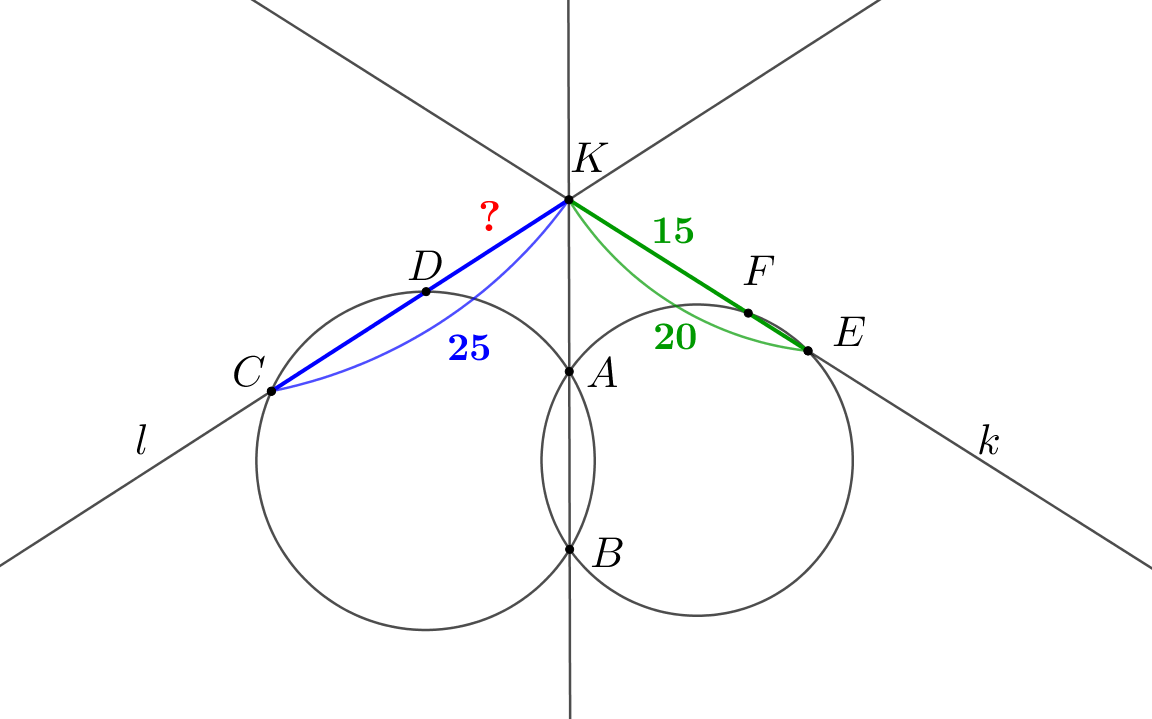
Дважды воспользуемся правилом:
Теорема об отрезках секущих
Если две секущие проходят через одну точку, то произведение отрезков одной секущей равно произведению отрезков другой секущей:
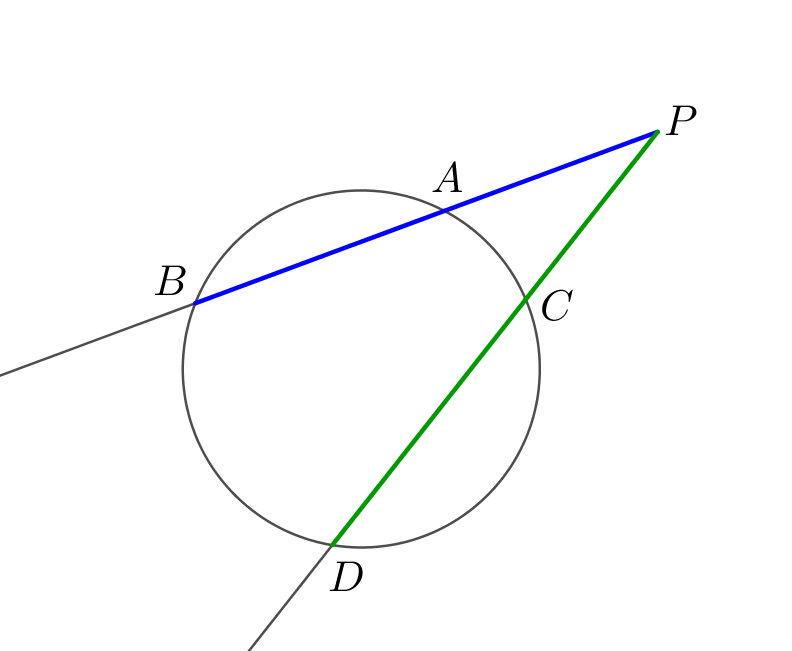
\(\displaystyle \color{blue}{AP}\cdot \color{blue}{BP}=\color{green}{CP}\cdot \color{green}{ DP}\)
\(\displaystyle \color{blue}{CK} \cdot \color{blue}{DK}=\color{orange}{AK}\cdot \color{orange}{BK}\small.\)
\(\displaystyle \color{green}{EK}\cdot \color{green}{FK}=\color{orange}{AK}\cdot \color{orange}{BK}\small.\)
Тогда и
\(\displaystyle \color{blue}{CK} \cdot \color{blue}{DK}=\color{green}{EK}\cdot \color{green}{FK}\small.\)
Подставляя известные значения\(\displaystyle KC=25,\,KE=20,\,KF=15{\small:}\)
\(\displaystyle 25\cdot KD=20\cdot15\small,\)
\(\displaystyle KD=\frac{20\cdot15}{25}=12\small.\)
Ответ: \(\displaystyle KD=12\small.\)