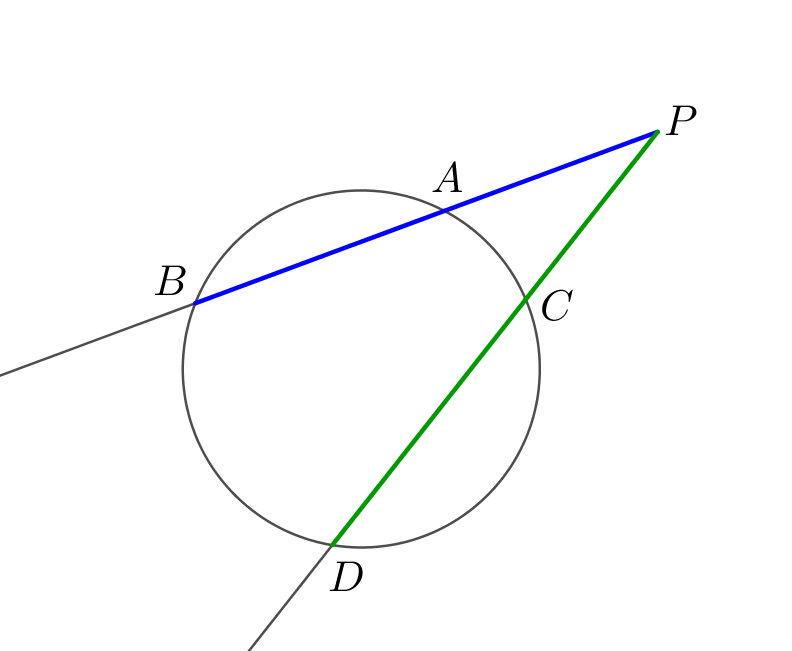
Из точки \(\displaystyle P\small,\) лежащей вне окружности, провели две секущие. Одна секущая пересекает окружность в точках \(\displaystyle A\) и \(\displaystyle B\small,\) другая в точках \(\displaystyle C\) и \(\displaystyle D\small.\) Известно, что \(\displaystyle PA:PB=PC:PD=1:3\) и \(\displaystyle PB=9\small.\) Найдите \(\displaystyle PC\small.\)
По условию \(\displaystyle PA:PB=PC:PD=1:3\small.\) Тогда \(\displaystyle PB=3PA\) и \(\displaystyle PD=3PC\small.\) | 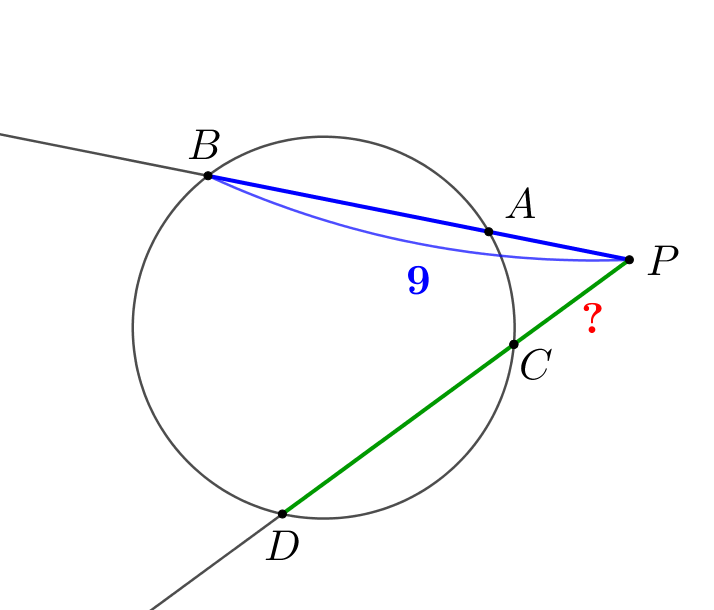 |
\(\displaystyle \color{blue}{PA}\cdot \color{blue}{PB}=\color{green}{PC}\cdot \color{green}{PD}\small.\)
Подставляя \(\displaystyle PB=3PA\) и \(\displaystyle PD=3PC\small,\) получаем:
\(\displaystyle PA\cdot 3PA=PC\cdot 3PC\small,\)
\(\displaystyle 3PA^2=3PC^2\small.\)
Значит,
\(\displaystyle PA=PC{ \small ,}\) откуда и \(\displaystyle PB=PD\small.\)
По условию \(\displaystyle PB=9\small.\) Тогда
\(\displaystyle PC=PA=\frac{PB}{3}=\frac{9}{3}=3\small.\)
Ответ: \(\displaystyle PC=3\small.\)