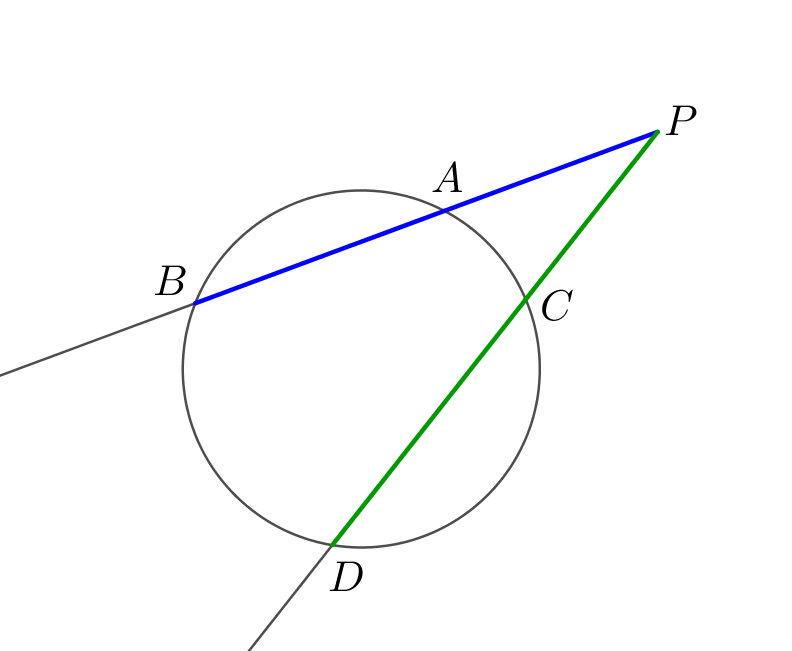
Две окружности имеют один центр – точку \(\displaystyle O\small,\) а их радиусы относятся как \(\displaystyle 1:2\small.\) Хорда большей окружности делится меньшей окружностью на три равные части. Найдите отношение длины этой хорды к диаметру меньшей окружности.
Обозначим радиус маленькой окружности за \(\displaystyle x\small.\) Радиус большей окружности в два раза больше, то есть \(\displaystyle 2x\small.\) Обозначим треть длины хорды за \(\displaystyle y\small.\) Необходимо найти отношение длины хорды к диаметру меньшей окружности, то есть \(\displaystyle \frac{3y}{2x}\small.\) | 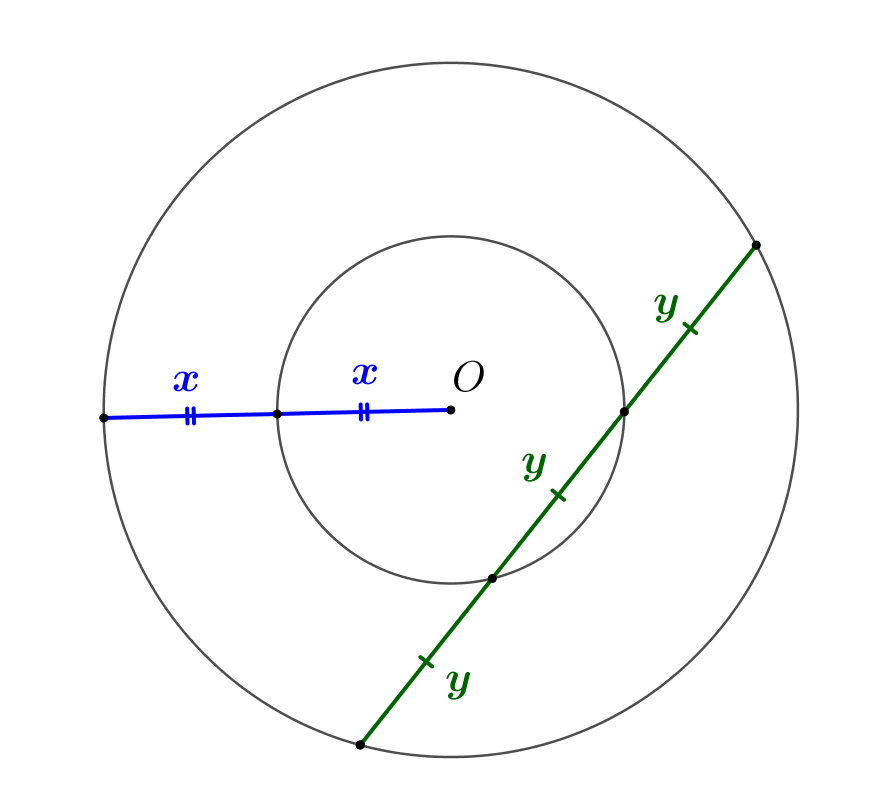 |
Проведем через один из концов хорды секущую маленькой окружности, проходящую через центр окружностей.
Тогда отрезки секущих равны:
| 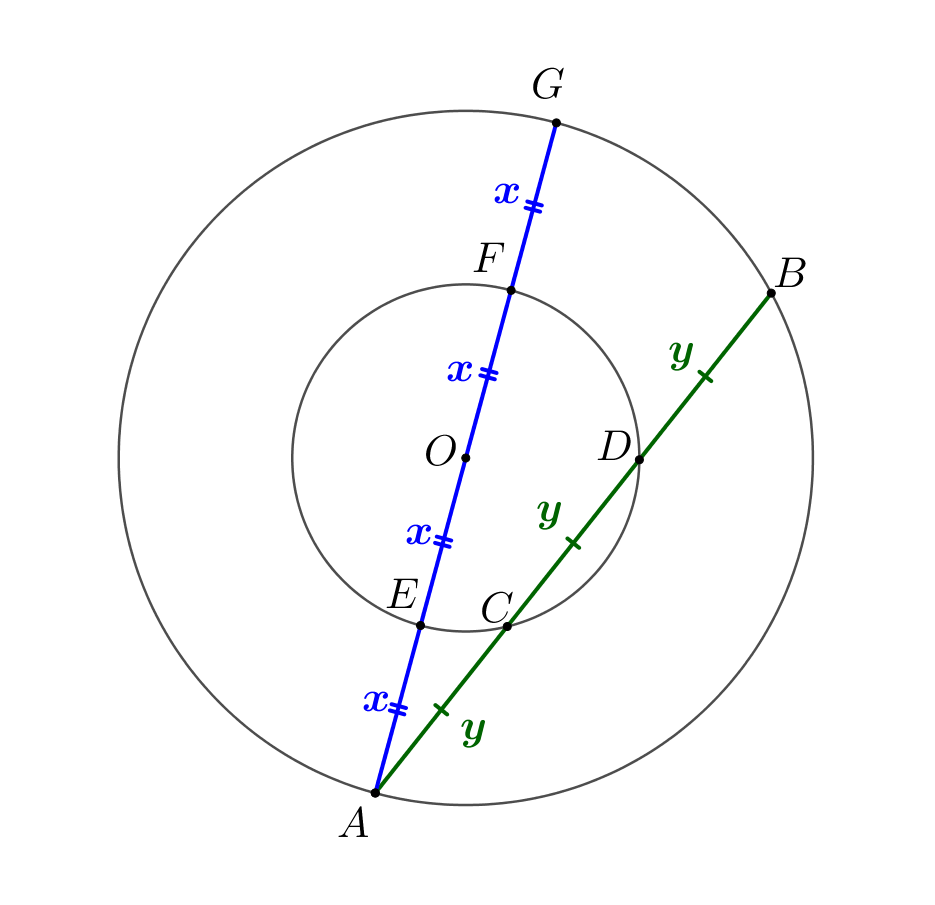 |
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{AF}=\color{green}{AC}\cdot \color{green}{AD}\small.\)
Подставляя отрезки секущих, получаем:
\(\displaystyle y\cdot 2y=x\cdot3x\small.\)
Откуда найдем отношение \(\displaystyle y\) к \(\displaystyle x{\small:}\)
\(\displaystyle 2y^2=3x^2\small,\)
\(\displaystyle \frac{y^2}{x^2}=\frac{3}{2}\small.\)
Поскольку \(\displaystyle x\) и \(\displaystyle y\) длины отрезков и неотрицательны, то
\(\displaystyle \frac{y}{x}=\sqrt{\frac{3}{2}}\small.\)
Тогда
\(\displaystyle \frac{AB}{EF}=\frac{3y}{2x}=\frac{3}{2}\cdot\frac{y}{x}=\frac{3}{2}\cdot\sqrt{\frac{3}{2}}=\frac{3\sqrt{3}}{2\sqrt{2}}\small.\)
Ответ: \(\displaystyle \frac{3\sqrt{3}}{2\sqrt{2}}\small.\)