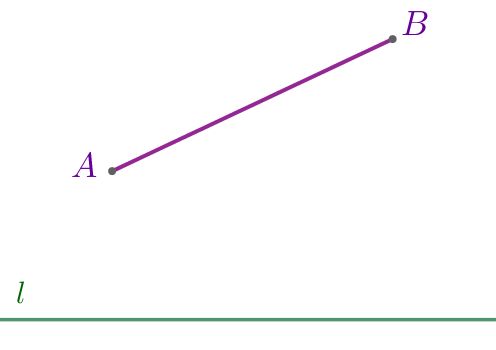
Концы отрезка \(\displaystyle AB\) лежат по одну сторону от прямой \(\displaystyle l{\small.}\) Расстояние от точки \(\displaystyle A\) до прямой \(\displaystyle l\) равно \(\displaystyle 24{\small,}\) а расстояние от точки \(\displaystyle B\) до прямой \(\displaystyle l\) равно \(\displaystyle 62{\small.}\) Найдите расстояние от середины отрезка \(\displaystyle AB\) до прямой \(\displaystyle l{\small.}\)
Расстояние от точки до прямой равно длине перпендикуляра, проведённого из этой точки к данной прямой. Пусть:
- \(\displaystyle AD\) – перпендикуляр, проведённый из точки \(\displaystyle A\) к прямой \(\displaystyle l{\small;}\)
- \(\displaystyle BC\) – перпендикуляр, проведённый из точки \(\displaystyle B\) к прямой \(\displaystyle l{\small.}\)
Изобразим предложенную в задаче конструкцию в виде прямоугольной трапеции \(\displaystyle ABCD{\small:}\)
Требуется найти длину \(\displaystyle MN{\small.}\) | 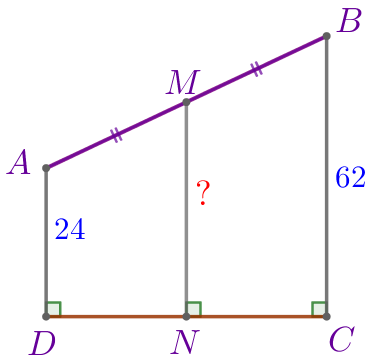 |
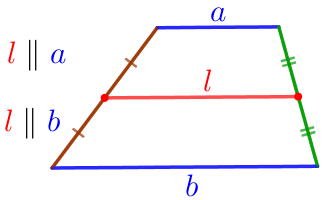
\(\displaystyle MN\) – средняя линия трапеции \(\displaystyle ABCD{\small.}\)
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 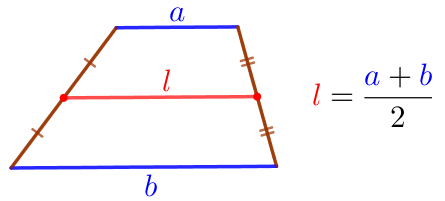 |
Следовательно,
\(\displaystyle MN=\frac{AD+BC}{2}=\frac{24+62}{2}=\frac{86}{2}=43{\small.}\)
Ответ: \(\displaystyle 43{\small .}\)