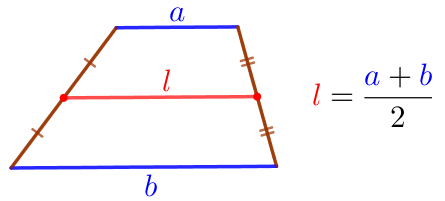
Основания \(\displaystyle BC\) и \(\displaystyle AD\) трапеции \(\displaystyle ABCD\) равны соответственно \(\displaystyle 8\) и \(\displaystyle 14{\small.}\) Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции диагональ \(\displaystyle BD{\small.}\)
\(\displaystyle ABCD\) – трапеция:
| 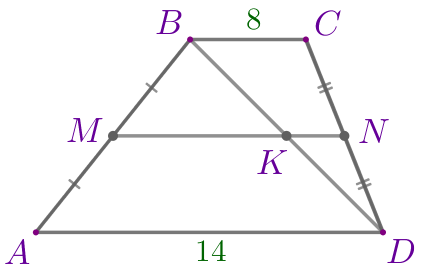 |
Требуется найти меньший из отрезков \(\displaystyle MK\) и \(\displaystyle KN{\small.}\)
\(\displaystyle MN=11{\small.}\)
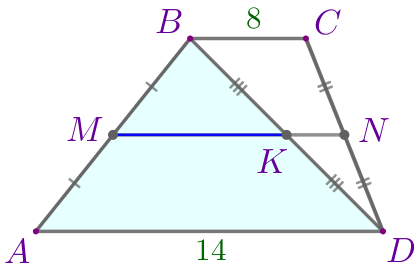
Рассмотрим треугольник \(\displaystyle ABD{\small.}\)
 |
|
\(\displaystyle MK\) – средняя линия треугольника \(\displaystyle ABD{\small.}\)
По свойству средней линии треугольника \(\displaystyle MK=\frac{1}{2} \cdot AD=\frac{1}{2} \cdot 14=7{\small.}\) Поскольку точка \(\displaystyle K\) лежит на \(\displaystyle MN{\small,}\) то \(\displaystyle KN=MN-MK=11-7=4{\small.}\) | 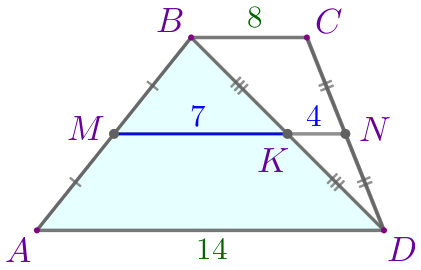 |
Диагональ \(\displaystyle BD\) делит среднюю линию \(\displaystyle MN\) трапеции \(\displaystyle ABCD\) на отрезки
\(\displaystyle MK=7\) и \(\displaystyle KN=4{\small.}\)
Длина меньшего из них равна \(\displaystyle 4{\small.}\)
Ответ: \(\displaystyle 4{\small .}\)