Средняя линия трапеции равна \(\displaystyle 9{\small,}\) разность оснований равна \(\displaystyle 4{\small.}\) Найдите меньшее основание трапеции.
По условию средняя линия трапеции равна \(\displaystyle \color{green}{9}{\small.}\) Пусть \(\displaystyle \color{blue}{a}\) – меньшее основание трапеции, тогда \(\displaystyle \color{blue}{a+4}\) – большее основание трапеции. | 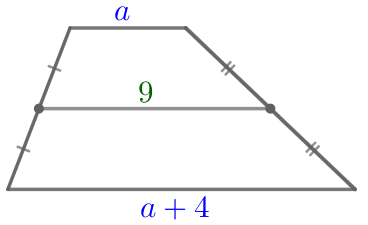 |
Требуется найти меньшее основание трапеции.
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 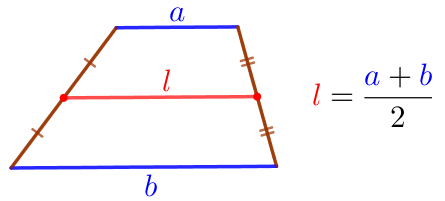 |
Согласно теореме
\(\displaystyle \color{green}{9}=\frac{\color{blue}{a}+(\color{blue}{a+4})}{2}{\small.}\)
Решим полученное уравнение и найдём \(\displaystyle \color{blue}{a}{\small:}\)
\(\displaystyle 9=\frac{2\color{blue}{a}+4}{2}{\small;}\)
\(\displaystyle 2\color{blue}{a}+4=18{\small;}\)
\(\displaystyle 2\color{blue}{a}=14{\small;}\)
\(\displaystyle \color{blue}{a}=7{\small.}\)
Меньшее основание трапеции равно \(\displaystyle 7{\small.}\)
Ответ: \(\displaystyle 7{\small .}\)