Средняя линия трапеции больше одного из оснований на \(\displaystyle 5{\small.}\) Найдите разность большего и меньшего оснований данной трапеции.
Пусть
Средняя линия не может быть больше большего основания, значит, средняя линия больше на \(\displaystyle 5\) меньшего основания:
| 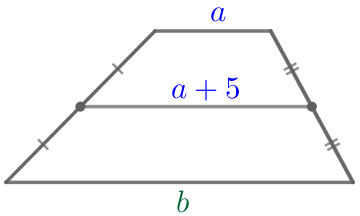 |
Требуется найти разность большего и меньшего оснований данной трапеции, то есть:
\(\displaystyle \Delta= \color{green}{b}-\color{blue}{a}=\color{red}{\large ?}\)
Средняя линия трапеции параллельна её основаниям и равна половине их суммы. | 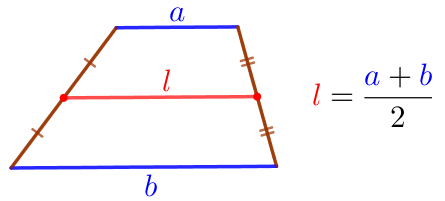 |
Согласно теореме
\(\displaystyle \color{blue}{a+5}=\frac{\color{blue}{a}+\color{green}{b}}{2}{\small.}\)
Выразим \(\displaystyle \color{green}{b}\) через \(\displaystyle \color{blue}{a}{\small:}\)
\(\displaystyle 2\color{blue}{a}+10=\color{blue}{a}+\color{green}{b}{\small;}\)
\(\displaystyle \color{green}{b}=\color{blue}{a}+10{\small.}\)
Тогда
\(\displaystyle \Delta= \color{green}{b}-\color{blue}{a}=(\color{blue}{a}+10)-\color{blue}{a}=\cancel{\color{blue}{a}}+10-\cancel{\color{blue}{a}}=10{\small.}\)
Разность оснований равна \(\displaystyle 10{\small.}\)
Ответ: \(\displaystyle 10{\small .}\)