Отрезок \(\displaystyle KM\) длиной \(\displaystyle 77\,{\footnotesize см}\) разделён точкой \(\displaystyle L\) на две части.
Известно отношение длин этих частей: \(\displaystyle KL:LM=9:5{\small .}\)

Найдите длину отрезка \(\displaystyle KL{\small .}\) Ответ дайте в миллиметрах.
\(\displaystyle KL=\)\(\displaystyle {\footnotesize мм}\)
Отрезок \(\displaystyle KM\) делится точкой \(\displaystyle L\) в отношении \(\displaystyle 9:5{\small ,}\) считая от точки \(\displaystyle K{\small .}\)
Это означает, что если отрезок \(\displaystyle KM\) разбить на \(\displaystyle 9+5=14\) равных частей, то:
- точка \(\displaystyle L\) окажется в \(\displaystyle 9\) частях такого разбиения от точки \(\displaystyle K\);
- точка \(\displaystyle L\) окажется в \(\displaystyle 5\) частях такого разбиения от точки \(\displaystyle M\).
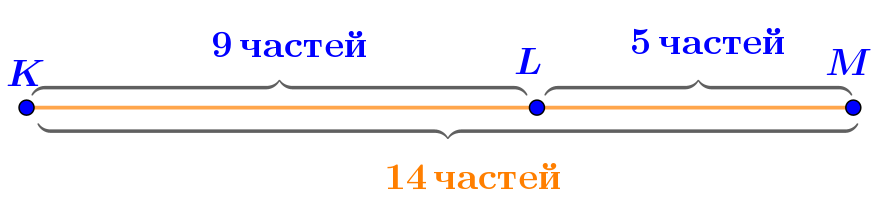
Значит, длина отрезка \(\displaystyle KL\) составляет \(\displaystyle \frac {{9}}{{14}}\) длины отрезка \(\displaystyle KM{\small .}\)
Длина отрезка \(\displaystyle KM\) равна \(\displaystyle 77 ~{\footnotesize см}{\small .}\)
Вычислим длину отрезка \(\displaystyle KL\) в сантиметрах:
\(\displaystyle KL=\frac {9}{14} \cdot KM= \frac {9}{14} \cdot 77= \frac {99}{2} \;{\footnotesize (см)}{\small .}\)
Поскольку в \(\displaystyle 1\) сантиметре содержится \(\displaystyle 10\) миллиметров,
\(\displaystyle KL= \frac {{99 }}{{2}}\cdot {10} = 495\,{\footnotesize (мм)}{\small .}\)
Ответ: \(\displaystyle 495\,{\footnotesize мм}{\small .}\)