На прямой \(\displaystyle p\) отметили несколько точек. При этом образовались обозначенные равные отрезки.

Рассмотрим произвольную точку \(\displaystyle M\) этой же прямой, от которой расстояние до точки \(\displaystyle B\) не меньше, чем расстояние до точки \(\displaystyle F{\small : }\)
\(\displaystyle MB\geqslant MF{\small .}\)
Какую фигуру заполняют точки \(\displaystyle M{\small ,}\) обладающие этим свойством? Выберите название и правильно обозначьте фигуру.
\(\displaystyle ~\)
Требуется, чтобы расстояние от точки \(\displaystyle M \) до точки \(\displaystyle B \) было не меньше, чем расстояние до точки \(\displaystyle F{\small : }\)
\(\displaystyle MB\geqslant MF{\small .}\)
Рассмотрим разные положения точки \(\displaystyle M\) на прямой \(\displaystyle p\).
Удобно исследовать части прямой, "перемещая" точку \(\displaystyle M\) по прямой слева направо.
Далее используем тот факт, что точка \(\displaystyle D\)– середина отрезка \(\displaystyle BF{\small .} \) Тогда длины \(\displaystyle BD \) и \(\displaystyle DF \) равны.
Отмечая на прямой все найденные точки и области, получаем луч \(\displaystyle DF{\small :}\)

Представить себе сделанный в решении пребор точек проще, глядя на анимацию этого процесса:
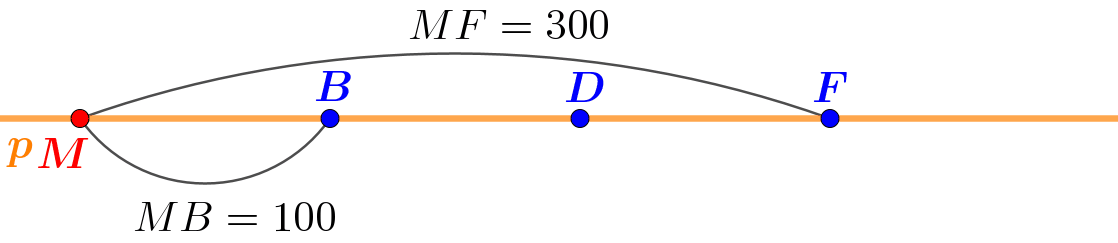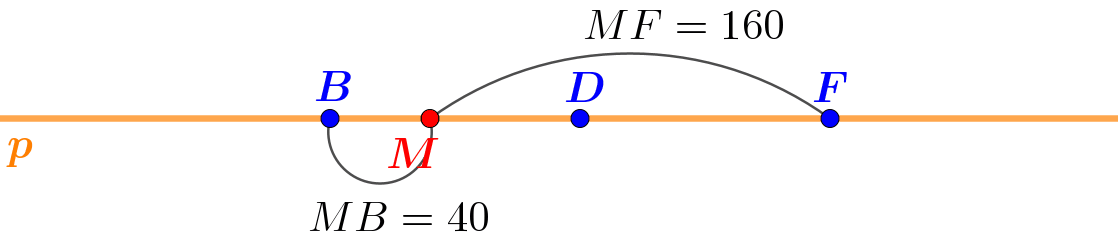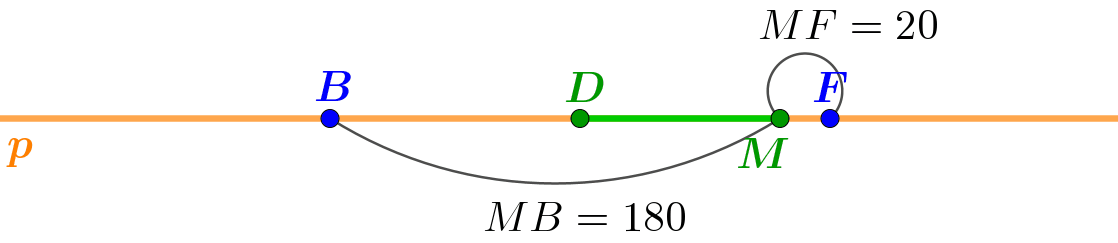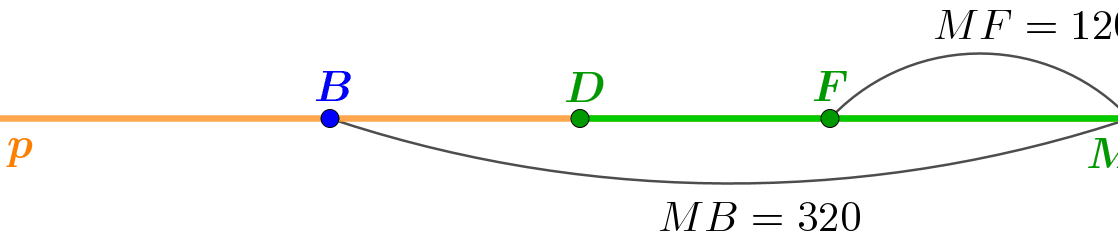
Ответ: луч \(\displaystyle DF \; (DE){\small .}\)




