На рисунке \(\displaystyle \angle 1= 58^{\circ}{\small,}\) \(\displaystyle \angle 2= 134^{\circ}{\small,}\) \(\displaystyle \angle 4= 58^{\circ}{\small.}\)
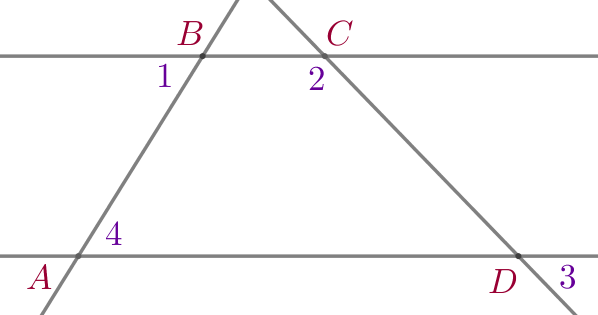
Найдите угол \(\displaystyle 3{\small.}\) Ответ дайте в градусах.
\(\displaystyle \angle 3=\) \(\displaystyle ^{\circ}{\small.}\)
Обозначим на рисунке величины известных углов.
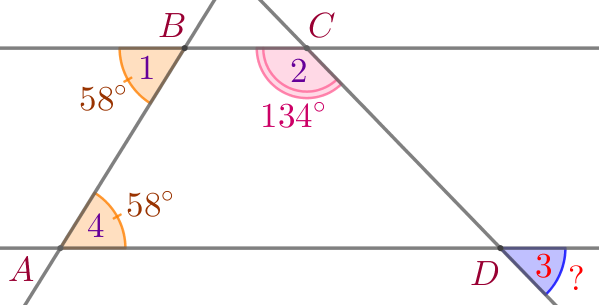
| Если две прямые пересечены секущей, и накрест лежащие углы равны, то эти прямые параллельны. | 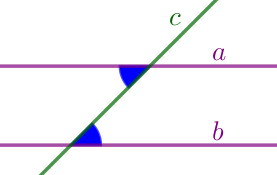 |
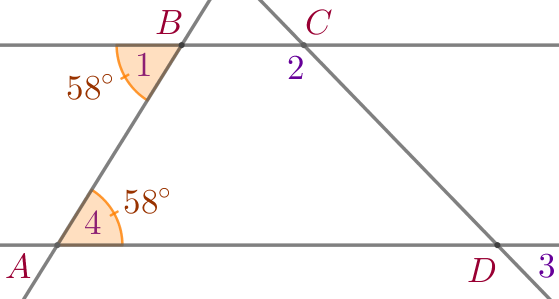 | \(\displaystyle \angle 1\) и \(\displaystyle \angle 4\) – накрест лежащие углы при прямых \(\displaystyle AD\) и \(\displaystyle BC\) и секущей \(\displaystyle AB{\small.}\) Так как \(\displaystyle \angle 1=\angle 4=58^{\circ}{\small,}\) то \(\displaystyle AD \parallel BC{\small.}\) |
\(\displaystyle \angle ADC= 46^{\circ}{\small.}\)
| Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов. | 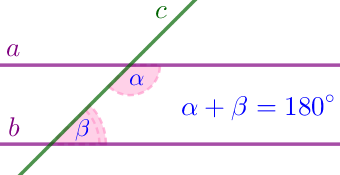 |
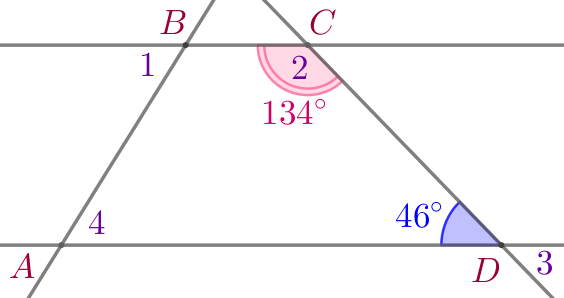 | \(\displaystyle \angle ADC\) и \(\displaystyle \angle 2\) – односторонние углы при параллельных прямых \(\displaystyle AD\) и \(\displaystyle BC\) и секущей \(\displaystyle CD{\small,}\) значит, \(\displaystyle \angle ADC+\angle 2=180^{\circ}{\small.}\) |
Следовательно,
\(\displaystyle \angle ADC=180^{\circ}-\angle 2=180^{\circ}-134^{\circ}=46^{\circ}{\small.}\)
\(\displaystyle \angle 3= 46^{\circ}{\small.}\)
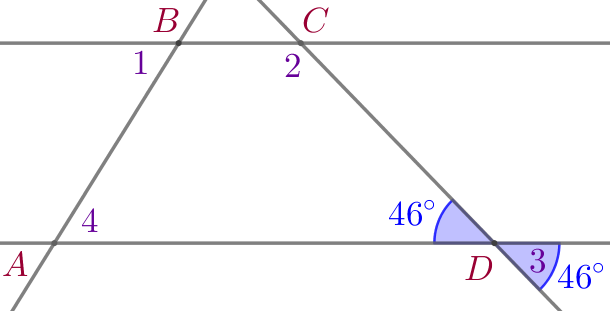 | \(\displaystyle \angle 3\) и \(\displaystyle \angle ADC\) – вертикальные углы, значит, \(\displaystyle \angle 3=\angle ADC=46^{\circ}{\small.}\) |
Ответ: \(\displaystyle \angle 3=46^{\circ}{\small.}\)