Основание \(\displaystyle AD\) прямоугольной трапеции \(\displaystyle ABCD\) с прямым углом \(\displaystyle A\) равно \(\displaystyle 12\small.\) Найдите длину вектора \(\displaystyle \overrightarrow{BD}\small,\) если \(\displaystyle AB=5\) и \(\displaystyle \angle D=45^{\circ}\small.\)
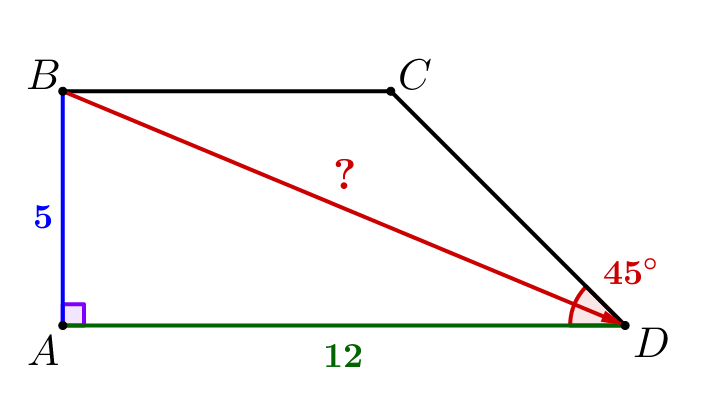
Длиной вектора \(\displaystyle \overrightarrow{AB}\) называется длина отрезка \(\displaystyle AB\small.\)
Длина вектора равна длине соответствующего отрезка. Тогда найдем длину отрезка \(\displaystyle BD\small.\)
Отрезок \(\displaystyle BD\) – гипотенуза в прямоугольном треугольнике \(\displaystyle ABD\small.\) Тогда по теореме Пифагора: \(\displaystyle BD^2=AB^2+AD^2=5^2+12^2=169\small,\) \(\displaystyle BD=\sqrt{169}=13\small.\) То есть \(\displaystyle \left|\overrightarrow{BD}\right|=BD=13\small.\) | 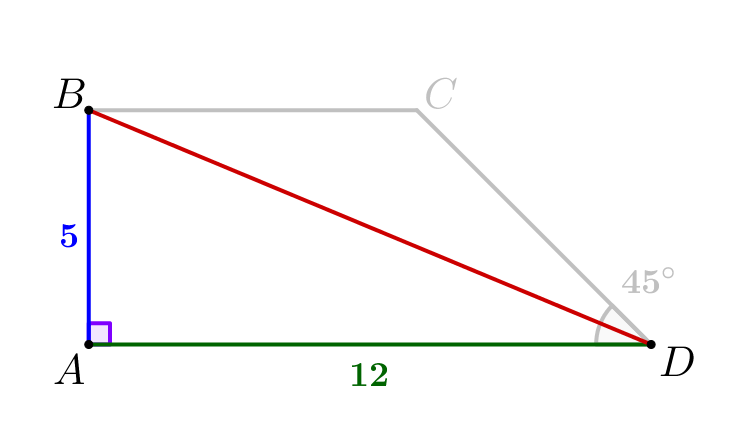 |
Ответ: \(\displaystyle \left|\overrightarrow{BD}\right|=13\small.\)