Диагонали прямоугольника \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle M\small.\) Найдите длину вектора \(\displaystyle \overrightarrow{MC}\small,\) если \(\displaystyle AB=4\) и \(\displaystyle BC=5\small.\)
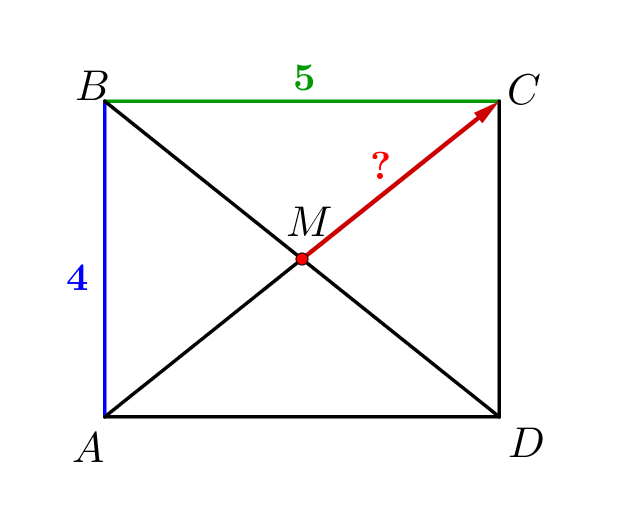
Длиной вектора \(\displaystyle \overrightarrow{AB}\) называется длина отрезка \(\displaystyle AB\small.\)
Длина вектора равна длине соответствующего отрезка. Тогда найдем длину отрезка \(\displaystyle MC\small.\)
Отрезок \(\displaystyle AC\) – гипотенуза прямоугольного треугольника \(\displaystyle ABC\small.\) Тогда по теореме Пифагора \(\displaystyle AC^2=AB^2+BC^2=4^2+5^2=41\small,\) \(\displaystyle AC=\sqrt{41}\small.\) Диагонали в прямоугольнике делятся точкой пересечения пополам. Значит, \(\displaystyle MC=\frac{AC}{2}=\frac{\sqrt{41}}{2}\small.\) | 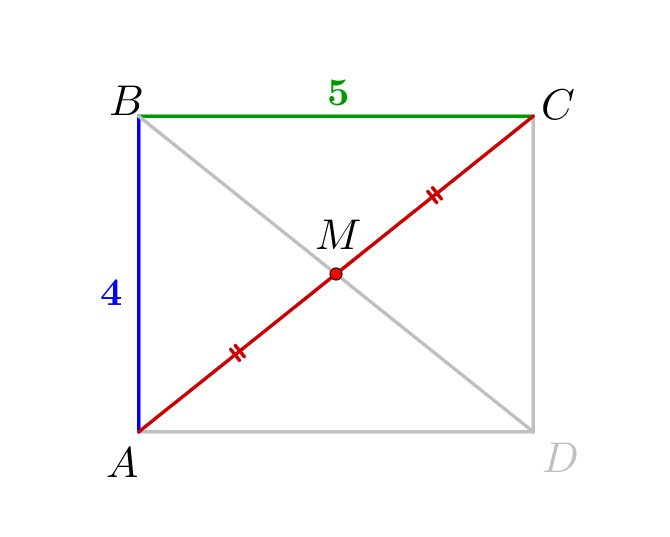 |
То есть
\(\displaystyle \left|\overrightarrow{MC}\right|=MC=\frac{\sqrt{41}}{2}\small.\)
Ответ: \(\displaystyle \left|\overrightarrow{MC}\right|=\frac{\sqrt{41}}{2}\small.\)