На рисунке проведена прямая \(\displaystyle a{\small ,}\) которая проходит через точку \(\displaystyle C{\small ,}\) и отмечено несколько точек.
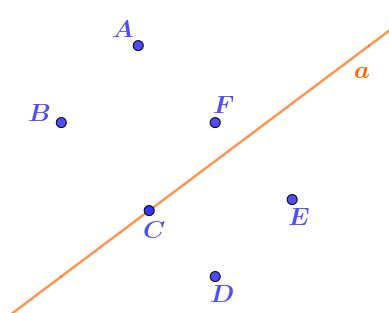
Сколько из отмеченных точек лежат в той полуплоскости с границей \(\displaystyle a{\small ,}\) которая не содержит точку \(\displaystyle D\;{\text ?}\)
Пусть точка \(\displaystyle A\) не принадлежит прямой \(\displaystyle a{\small .}\)
Полуплоскостью с границей \(\displaystyle a\) называется часть плоскости, содержащая все точки прямой \(\displaystyle a{\small ,}\) а также все точки плоскости, лежащие по одну сторону от этой прямой с точкой \(\displaystyle A{\small .}\)
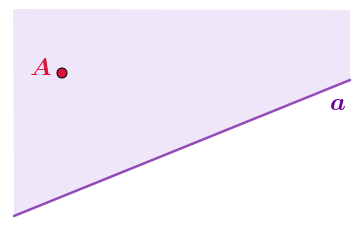
На рисунке выделена одна из двух полуплоскостей, на которые плоскость делится прямой \(\displaystyle a{\small .}\)
Каждая прямая делит плоскость на две полуплоскости.
Две точки принадлежат одной и той же полуплоскости с границей \(\displaystyle a\) тогда и только тогда, когда они лежат по одну сторону от прямой \(\displaystyle a{\small .}\)
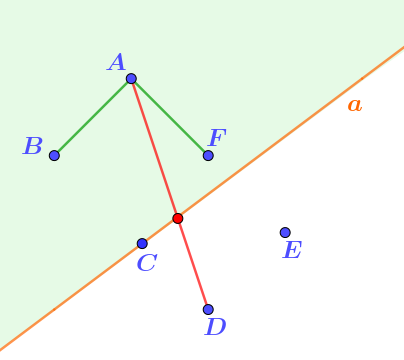
Найдём точку, лежащую с точкой \(\displaystyle D\) по разные стороны от прямой \(\displaystyle a{\small .}\) Это, к примеру, точка \(\displaystyle A{\small ,}\) так как отрезок \(\displaystyle AD\) пересекает прямую \(\displaystyle a\) (видно по рисунку).
Выделим на рисунке часть плоскости, которую заполняют точки, лежащие по одну сторону прямой \(\displaystyle a\) с точкой \(\displaystyle A{\small .}\)
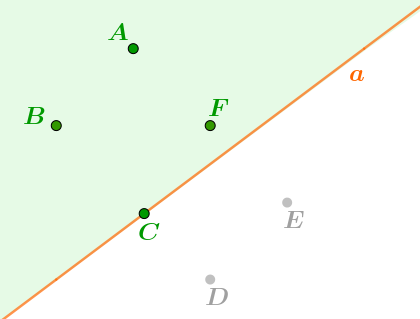
Всего насчитывается четыре точки, удовлетворяющие условию задачи: точки \(\displaystyle A{\small ,\;}B{\small ,\;}C\) и \(\displaystyle F{\small .}\)
Ответ: \(\displaystyle 4\) точки.