Какие из следующих утверждений верны?
Рассмотрим по очереди каждое из утверждений.
Об этом прямо написано в определении полуплоскости.
Пусть точка \(\displaystyle A\) не принадлежит прямой \(\displaystyle a{\small .}\)
Полуплоскостью с границей \(\displaystyle a\) называется часть плоскости, содержащая все точки прямой \(\displaystyle a{\small ,}\) а также все точки плоскости, лежащие по одну сторону этой прямой с точкой \(\displaystyle A{\small .}\)
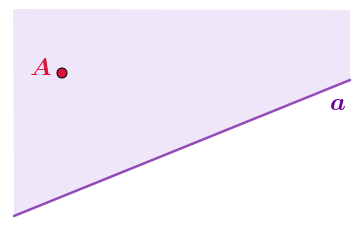
На рисунке выделена одна из двух полуплоскостей, на которые плоскость делится прямой \(\displaystyle a{\small .}\)
Согласно определению полуплоскости, любая точка общей границы двух полуплоскостей принадлежит каждой из этих полуплоскостей.
Возможны три случая расположения двух концов этого отрезка.
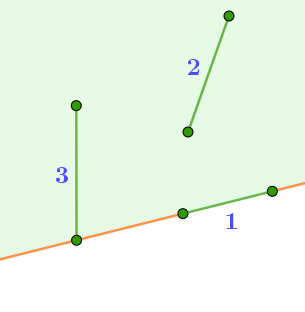
1. Оба конца отрезка на границе полуплоскости.
Тогда отрезок \(\displaystyle -\) часть границы полуплоскости и все его точки принадлежат полуплоскости.
2. Оба конца отрезка не принадлежат границе полуплоскости.
Тогда концы отрезка, согласно определению полуплоскости, расположены по одну сторону от границы.
Это, по определению, значит, что отрезок не пересекает границу. Значит, на отрезке нет ни одной точки, расположенной по разные стороны границы с одним из концов отрезка.
То есть все точки этого отрезка принадлежат полуплоскости.
3. Только один из концов отрезка принадлежит границе полуплоскости.
В этом случае прямая, содержащая отрезок, пересекает границу полуплоскости в единственной точке \(\displaystyle -\) конце отрезка.
Тогда другой отрезок, соединяющий внутреннюю точку исходного отрезка с не принадлежащим границе концом, не пересекает границу полуплоскости.
То есть внутренние точки исходного отрезка расположены по ту же сторону границы, что и один из концов. А значит, принадлежат полуплоскости.
Чтобы быть верным, утверждение должно выполняться при любом расположении рассматриваемого луча относительно полуплоскости.
То есть для опровержения достаточно найти расположение подходящего луча, для которого утверждение не выполнено.
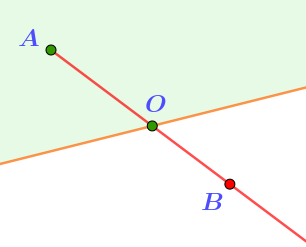
Возьмем две точки, скажем \(\displaystyle A\) и \(\displaystyle B{\small ,}\) по разные стороны границы полуплоскости.
Отрезок \(\displaystyle AB\) должен пересекать границу. Пусть это случилось в точке \(\displaystyle O{\small .}\)
На рисунке начало луча \(\displaystyle AB\) и его точка \(\displaystyle O\) принадлежат полуплоскости, но точка \(\displaystyle B\) этого луча полуплоскости не принадлежит.