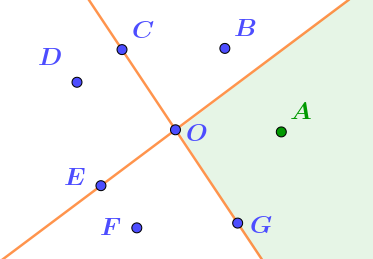
На рисунке отмечены несколько точек. Здесь же проведены две прямые. На одну из них попадают две отмеченных точки, на другую \(\displaystyle -\) три.
Прямые являются границами двух выделенных полуплоскостей.
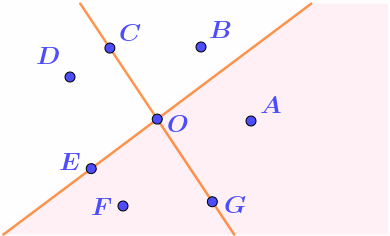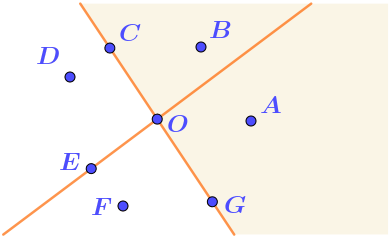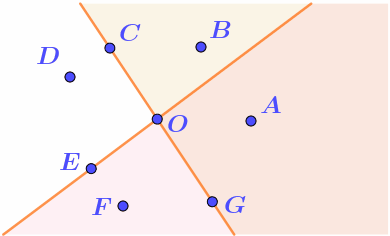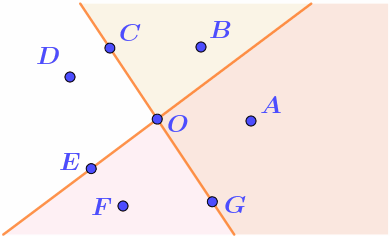
Найдите по одной точке, подходящей под каждое из данных описаний.
ОПИСАНИЕ ТОЧКИ
| ТОЧКА |
| Принадлежит обеим полуплоскостям, но ни одной из их границ. | |
| Не принадлежит ни одной из полуплоскостей. | |
| Принадлежит только одной полуплоскости и ни одной из границ полуплоскостей. | |
| Принадлежит границам обеих полуплоскостей. | |
| Принадлежит обеим полуплоскостям, но границе только одной из них. |
1. "Принадлежит обеим полуплоскостям, но ни одной из их границ". Принадлежность обеим полуплоскостям означает, что нужно рассматривать часть плоскости, заполненную общими точками полуплоскостей. Выделим её на рисунке. Из обозначенных точек туда попала только точка \(\displaystyle A{\small .}\) |
|
2. "Не принадлежит ни одной из полуплоскостей". Выделим на рисунке часть плоскости, точки которой не попадают ни в одну из полуплоскостей. Подходит только точка \(\displaystyle D{\small .}\) | 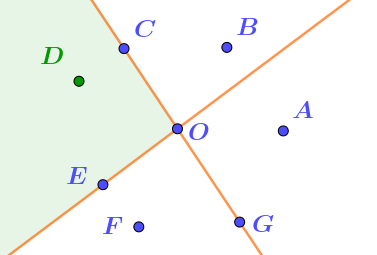 |
3. "Принадлежит только одной полуплоскости и ни одной из границ полуплоскостей". У нас две полуплоскости. Значит, нужно рассматривать только те их части, которые не пересекаются со второй полуплоскостью. Выделим эти части на рисунке. Поскольку точки также не должны лежать на границе полуплоскостей, то подходят точки \(\displaystyle B\) и \(\displaystyle F{\small .}\) | 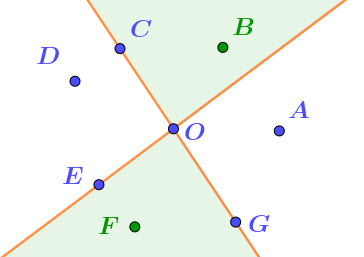 |
4. "Принадлежит границам обеих полуплоскостей". Границами данных по условию полуплоскостей являются прямые \(\displaystyle CG \)и\(\displaystyle OE{\small .} \) Принадлежит обеим границам только точка их пересечения \(\displaystyle O{\small .} \)
| 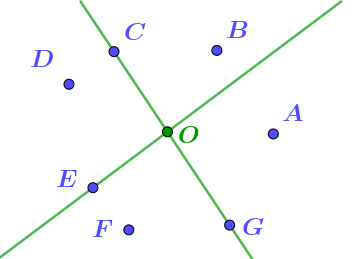 |
5. "Принадлежит обеим полуплоскостям, но границе только одной из них". То есть нужно найти пересечение выделенных полуплоскостей и взять точки на его границе. Выделим на рисунке. Подходит точка \(\displaystyle G{\small .} \) | 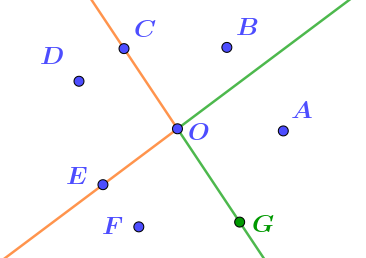 |
| Ответ: |  |