На плоскости отметили несколько точек так, что никакие три из них не принадлежат одной прямой.
Чтобы попарно соединить все эти точки понадобилось \(\displaystyle 10\) отрезков.
Из этих отрезков \(\displaystyle 6\) пересекли прямую \(\displaystyle p{\small ,}\) но ни один из концов отрезков на неё не попал.
Найдите наибольшее количество отмеченных точек, принадлежащих одной из полуплоскостей с границей \(\displaystyle p{\small .}\)
- Если бы точек было две, например, \(\displaystyle A\) и \(\displaystyle B{\small ,}\) то они соединялись бы одним отрезком.
- Добавление третьей точки увеличит число отрезков на два, до трёх. Это ясно: новую точку \(\displaystyle C\) нужно будет соединять с двумя исходными.
- Аналогично, добавление четвёртой точки \(\displaystyle D\) прибавит три отрезка. Общее число отрезков станет равным шести.
- Пятая точка \(\displaystyle E\) добавляет четыре отрезка и доводит счёт отрезков до десяти.

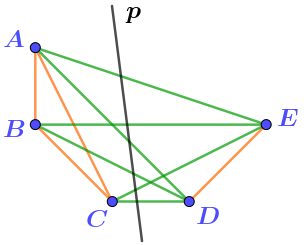
Продемонстрируем рисунок для случая, когда по одну сторону прямой \(\displaystyle p \) лежит три точки, а по другую – две.
Напомним, что прямую \(\displaystyle p \) должно пересекать \(\displaystyle 6 \) отрезков.
Покажем, что ни \(\displaystyle 4{ \small ,} \) ни тем более \(\displaystyle 5 \)точек не может лежать по одну сторону прямой \(\displaystyle p{\small .} \)
Для случая пяти точек все очевидно. В этом варианте все точки лежат по одну сторону прямой \(\displaystyle p{\small .} \) Значит, ни один из отрезков, соединяющих эти точки, не будет пересекать прямую \(\displaystyle p{\small .} \)
Рассмотрим случай, когда по одну сторону прямой \(\displaystyle p \) лежит \(\displaystyle 4 \)точки, а по другую \(\displaystyle 1 \) точка.
Тогда прямая будет пересекать только те отрезки, которые соединяют эту \(\displaystyle 1 \) точку с другими \(\displaystyle 4 \) точками. Таких отрезков будет \(\displaystyle 4{\small ,} \) а должно быть \(\displaystyle 6{\small .} \) Значит, этот случай также не подходит.
Ответ: \(\displaystyle 3\) точки.