На клетчатой бумаге изображены восемь четырёхугольников. Известно, что два из них равны.
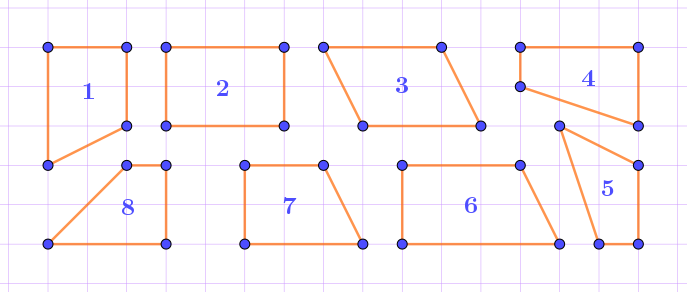
Найдите эту пару.
Четырёхугольник
Две фигуры равны, если их можно совместить наложением.
Ясно, что при наложении одного многоугольника на другой вершины первого совпадут с вершинами второго, и стороны первого совпадут со сторонами второго.
То есть наложение, совмещая многоугольники, совмещает и их элементы \(\displaystyle -\) вершины, стороны и углы.
Значит у двух равных многоугольников:
- количества вершин одинаковы;
- стороны попарно равны;
- углы попарно равны.
- В многоугольнике номер \(\displaystyle 2\) четыре прямых угла. Он единственный, обладающий этим свойством.
- В многоугольнике номер \(\displaystyle 3\) нет прямых углов. Он единственный, обладающий этим свойством.
- В многоугольнике номер \(\displaystyle 5\) ровно один прямой угол. Он единственный, обладающий этим свойством.
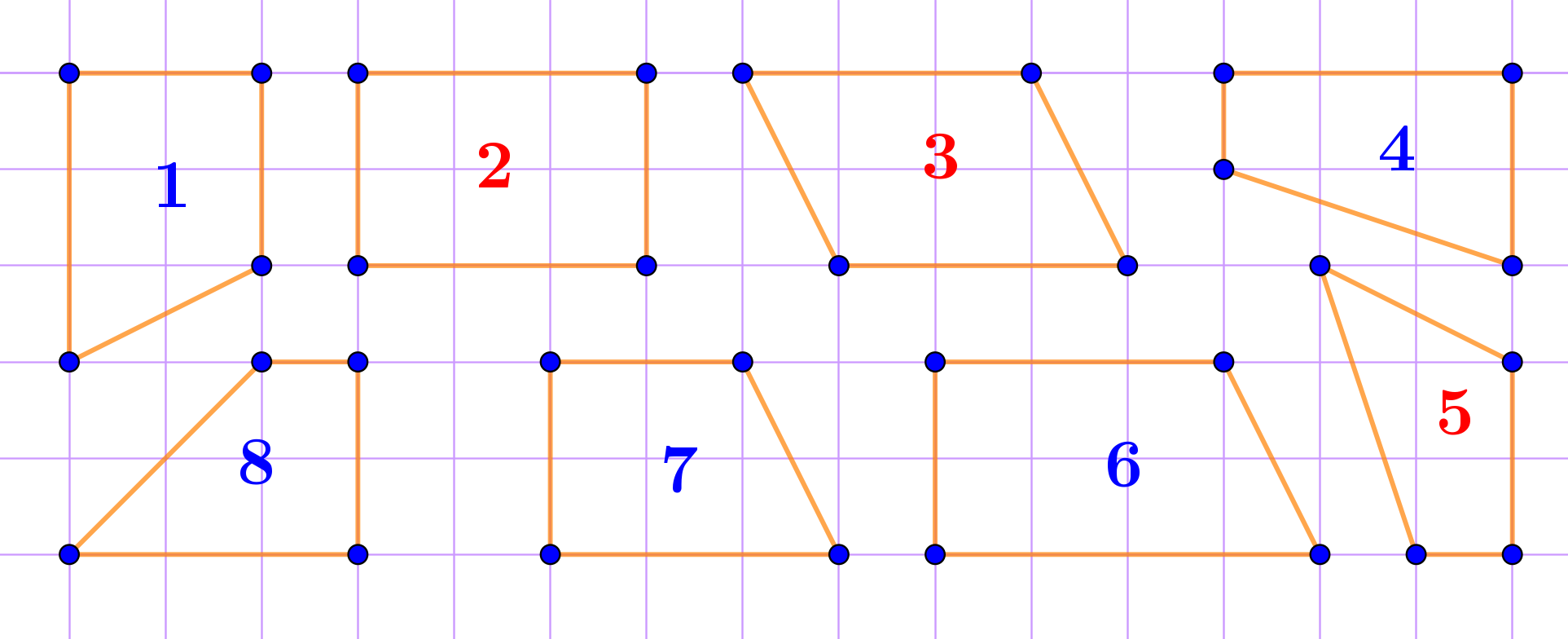
Все оставшиеся четырёхугольники имеют ровно два прямых угла. И пару равных нужно искать среди них.
В каждом из оставшихся многоугольников есть ровно одна сторона, не образующая прямых углов со смежными сторонами.
Вершины, углы при которых прямые, при совмещающем равные фигуры наложении, должны совмещаться. Значит, если удалить в равных четырёхугольниках сторону, соединяющую другие вершины, должны образовываться равные ломаные.
В частности, у равных четырёхугольников должны совпадать длины ломаных, полученных указанным способом.
Считаем по клеткам длины всех пяти ломаных и выясняем, что есть только две пары четырёхугольников, претендующих на равенство:
- первый и седьмой (длины ломаных равны семи клеткам);
- восьмой и четвёртый (длины ломаных равны шести клеткам).
При наложении равных четырёхугольников должны совмещаться стороны, прилежащие к двум прямым углам.
В каждом из оставшихся четырёхугольников такая сторона одна.
Но у четырёхугольника номер \(\displaystyle 8\) её длина равна двум клеткам, а у четырёхугольника номер \(\displaystyle 4\) её длина составляет три клетки.
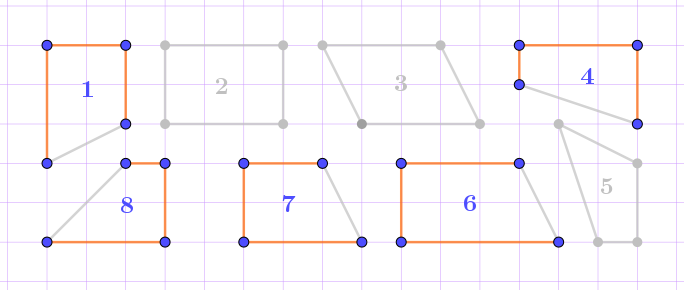
Остаётся только одна пара четырёхугольников, которые могут быть равными \(\displaystyle -\) первый и седьмой.
Ответ: четырёхугольник \(\displaystyle 7\) равен четырёхугольнику \(\displaystyle 1{\small .}\)