Задание
В треугольнике \(\displaystyle ABC\) все углы различны и все стороны различны.
Треугольники \(\displaystyle ABC\) и \(\displaystyle KLM\) равны.
На рисунке отмечены некоторые из их равных элементов.
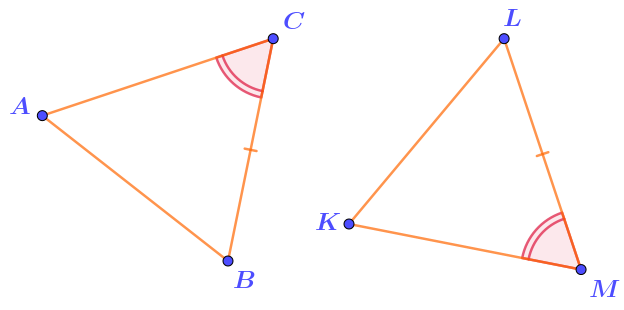
Выберите из предложенных равенств верные.
Решение
Дополним чертёж задачи, используя правила расположения равных элементов в равных треугольниках.
Равные треугольники
Две фигуры называются равными, если они совмещаются наложением.
Если два треугольника равны друг другу, то шесть элементов (три стороны и три угла) одного треугольника соответственно равны шести элементам другого треугольника.
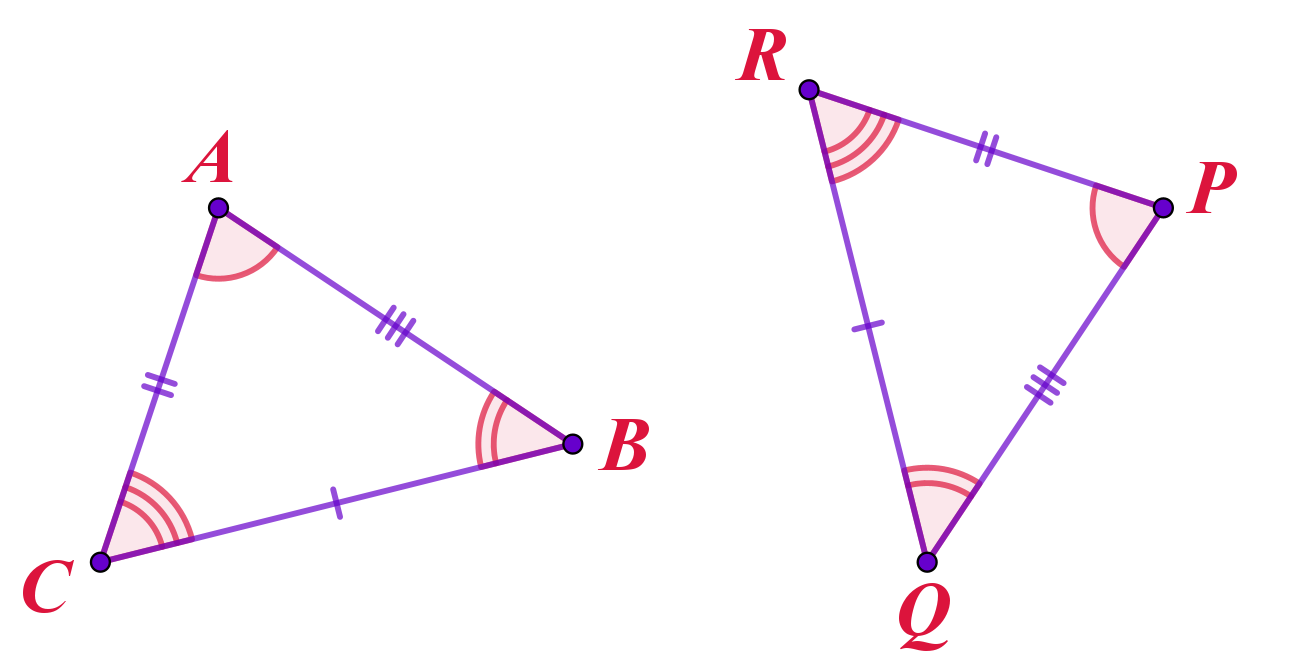
В равных треугольниках равные элементы всегда расположены так, как показано на рисунке:
- против равных сторон лежат равные углы;
- против равных углов лежат равные стороны.
- Обозначим как равные стороны \(\displaystyle AB\) и \(\displaystyle KL{\small ,}\) расположенные против равных углов, и углы \(\displaystyle BAC\) и \(\displaystyle LKM{\small ,}\) расположенные против равных сторон.
- После этого неотмеченными останутся только два угла и две стороны. Они, по свойству равных треугольников, также должны образовывать пары равных элементов.
В итоге, для каждого элемента одного треугольника найден равный ему элемент,принадлежащий другому треугольнику.
Согласно условию, равными могут быть только элементы, отмеченные как равные. Пользуясь рисунком, выберем верные утверждения из предложенных.
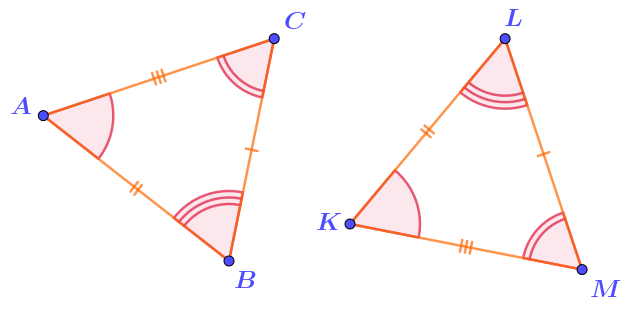
Неверные утверждения:
- \(\displaystyle AB=KM\)
- \(\displaystyle \angle CBA=\angle MKL\)
- \(\displaystyle AB=LM\)
Верные утверждения:
- \(\displaystyle \angle LMK=\angle ACB\)
- \(\displaystyle KM=AC\)
- \(\displaystyle \angle ABC=\angle KLM\)