На сторонах треугольника \(\displaystyle ABC\) построили три равных ему треугольника \(\displaystyle ACM{\small,}\;BCL\) и \(\displaystyle ABN{\small .}\)
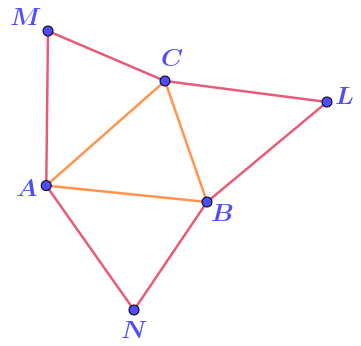
Периметр треугольника \(\displaystyle ABC\) равен \(\displaystyle 26{\small .}\)
Найдите периметр шестиугольника \(\displaystyle ANBLCM{\small .}\)
\(\displaystyle P_{ANBLCM}=\)
РЕШЕНИЕ 1
Два равных треугольника имеют три пары равных сторон.
Значит, и суммы длин их сторон (периметры) равных треугольников равны.
На рисунке четыре равных треугольника, но ровно три из них можно составить, использовав все отрезки рисунка.
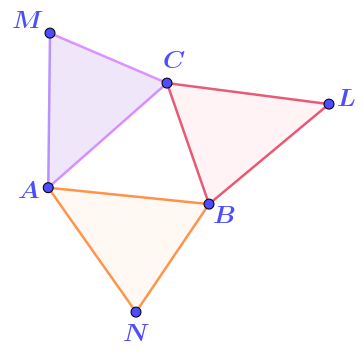
Значит, сумма длин всех отрезков равна утроенному периметру треугольника \(\displaystyle ABC{\text :}\)
\(\displaystyle AB+AC+BC+AM+CM+CL+BL+BN+AN=3\cdot P_{ABC}=3\cdot 26=78{\small .}\)
Все отрезки рисунка как раз составляют рассматриваемый шестиугольник и треугольник \(\displaystyle ABC{\small .}\)
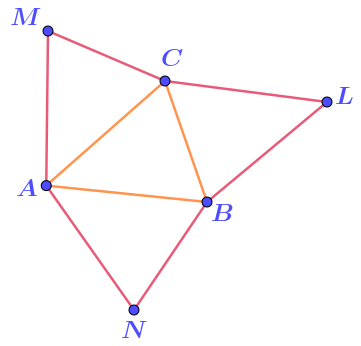
Значит, периметр шестиугольника равен разности суммы длин всех отрезков рисунка и периметра треугольника:
\(\displaystyle P_{ANBLCM}=78-P_{ABC}=78-26=52{\small .}\)
Ответ: \(\displaystyle 52{\small .}\)
РЕШЕНИЕ 2
Запишем сумму длин всех отрезков шестиугольника \(\displaystyle ANBLCM{\small :}\)
\(\displaystyle AN+NB+BL+LC+CM+MA{\small .}\)
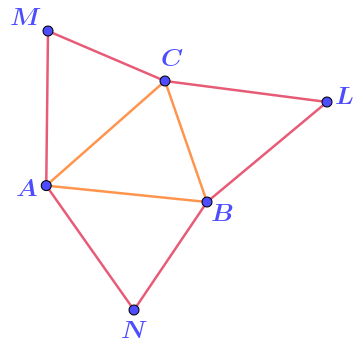
По условию, построенные треугольники равны треугольнику \(\displaystyle ABC{\small . } \) Например,
\(\displaystyle \triangle ABC=\triangle ANB{\small .}\)
У этих треугольников сторона \(\displaystyle AB\) общая, так что суммы длин двух других сторон равны:
\(\displaystyle AN+NB=AC+BC{\small .} \)
Аналогично,
\(\displaystyle BL+LC=AB+AC{\small ,} \)
\(\displaystyle AM+CM=AB+BC{\small .} \)
Используем полученные равенства, чтобы упростить выражение для периметра шестиугольника \(\displaystyle ANBLCM{\text :}\)
\(\displaystyle \begin{aligned}\color{green}{ AN}+\color{green}{ NB}+\color{blue}{ BL}+\color{blue}{ LC}+CM&+MA=\color{green}{ AC}+\color{green}{ BC}+\color{blue}{ AB}+\color{blue}{ AC}+AB+BC=\\[5px]&=2AC+2BC+2AB=2\cdot P_{ABC}=2\cdot 26=52{\small .}\end{aligned}\)
Ответ: \(\displaystyle 52{\small .}\)