В параллелограмме \(\displaystyle ABCD\) точка \(\displaystyle E\) – середина стороны \(\displaystyle AD\small,\) а \(\displaystyle F\) – середина \(\displaystyle AB\small.\)
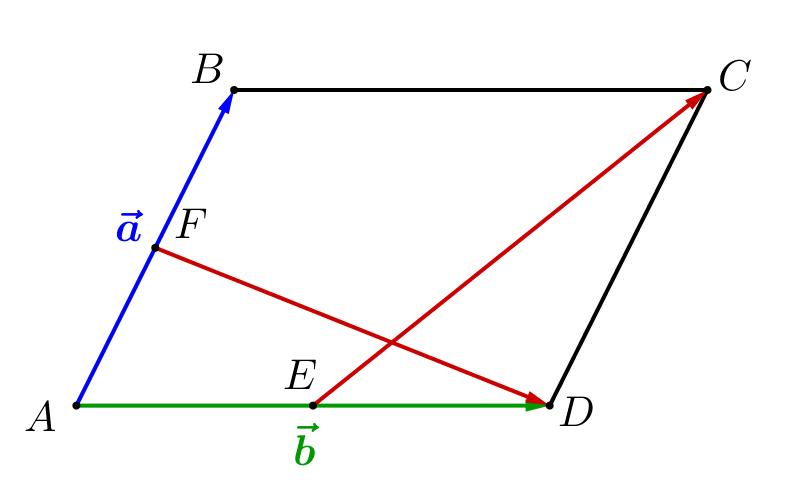
Обозначим векторы \(\displaystyle \overrightarrow{AB}=\vec{a}\) и \(\displaystyle \overrightarrow{AD}=\vec{b}\small.\) Выразите векторы \(\displaystyle \overrightarrow{FD}\) и \(\displaystyle \overrightarrow{EC}\) через \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}\small.\)
Вектор \(\displaystyle \overrightarrow{FD}\) равен сумме векторов: \(\displaystyle \overrightarrow{FD}=\overrightarrow{FA}+\overrightarrow{AD}\small.\) Вектор \(\displaystyle \overrightarrow{AD}\) равен \(\displaystyle \vec{b}\small.\) Вектор \(\displaystyle \overrightarrow{FA}\) противоположно направлен вектору \(\displaystyle \overrightarrow{AB}\) и в два раза короче. То есть \(\displaystyle \overrightarrow{FA}=-\frac{1}{2}\overrightarrow{AB}=-\frac{1}{2}\vec{a}\small.\) Значит, \(\displaystyle \overrightarrow{FD}=\overrightarrow{FA}+\overrightarrow{AD}=-\frac{1}{2}\vec{a}+\vec{b}\small.\) | 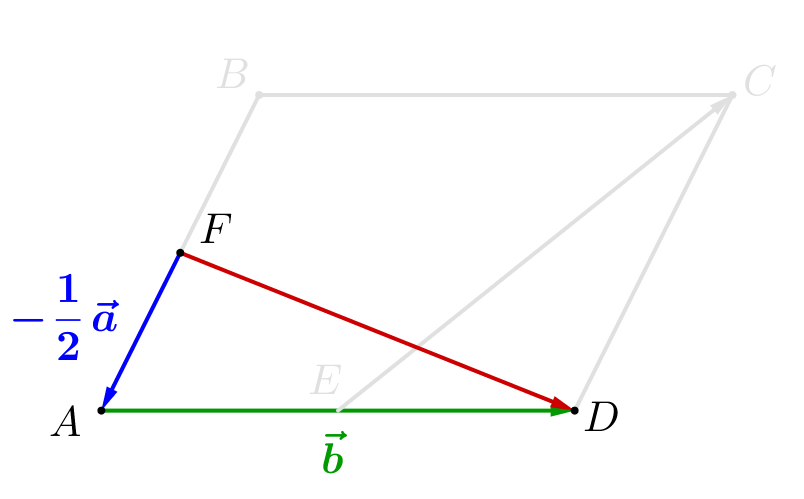 |
Вектор \(\displaystyle \overrightarrow{EC}\) равен сумме векторов: \(\displaystyle \overrightarrow{EC}=\overrightarrow{ED}+\overrightarrow{DC}\small.\) Вектор \(\displaystyle \overrightarrow{DC}\) сонаправлен вектору \(\displaystyle \overrightarrow{AB}\) и имеет такую же длину, то есть \(\displaystyle \overrightarrow{DC}=\overrightarrow{AB}=\vec{a}\small.\) Вектор \(\displaystyle \overrightarrow{ED}\) сонаправлен вектору \(\displaystyle \overrightarrow{AD}\) и в два раза короче. То есть \(\displaystyle \overrightarrow{ED}=\frac{1}{2}\overrightarrow{AD}=\frac{1}{2}\vec{b}\small.\) Значит, \(\displaystyle \overrightarrow{EC}=\overrightarrow{ED}+\overrightarrow{DC}=\frac{1}{2}\vec{b}+\vec{a}=\vec{a}+\frac{1}{2}\vec{b}\small.\) | 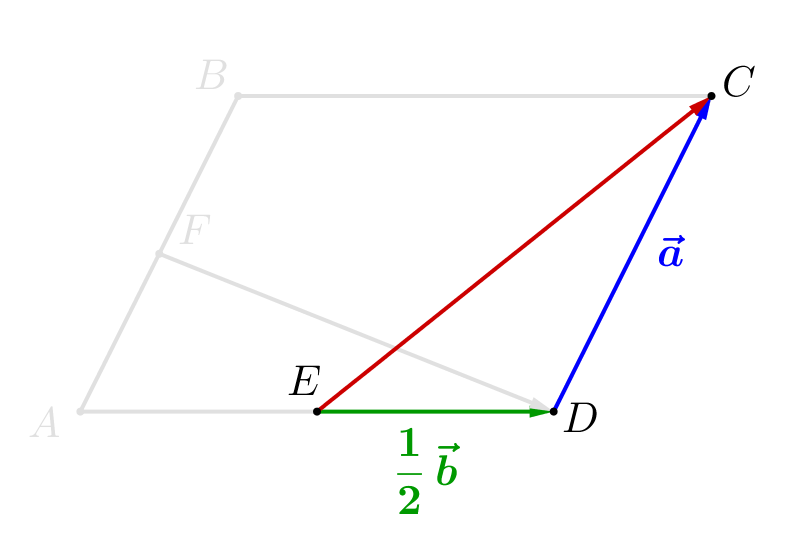 |